Dernière mise à jour le 23/09/2013

Présentation

Ce montage électronique permet de faire de la variation d’intensité lumineuse. La structure de l’ensemble est composé de composants passifs.

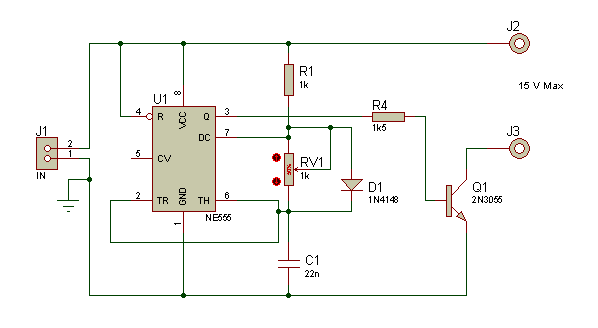
Schéma

Fonctionnement

Le circuit fait appel à un classique NE555 pour générer un signal périodique rectangulaire de fréquence “relativement” fixe, mais la largeur d’impulsions peut varier grâce au potentiomètre RV1.

L’oscillateur
L’oscillateur est bâtît sur un NE555 avec ses classiques composants satellites RV1, R2 et C1, dont les valeurs déterminent la fréquence d’oscillation et le rapport cyclique.

Interface de sortie
La sortie du NE555 (borne 3) n’est pas en mesure de délivrer un courant suffisant pour piloter directement une ampoule ou un moteur, aussi ce circuit intégré est-il épaulé par un transistor de puissance de type 2N3055, qui fait ainsi office d’interface de puissance. Le choix du transistor s’est porté sur un 2N3055 car ce dernier supporte bien des pointes de courant de plusieurs ampères. Sachez en effet qu’une ampoule électrique à filament, lorsqu’elle est éteinte, présente une résistance “à froid” dix à quinze fois inférieure à sa résistance “à chaud” (quand elle est allumée). Ainsi, une ampoule de 12W, qui consomme environ 1A en régime allumée, provoque une pointe de l’ordre de 10A lors de son allumage (ce à quoi l’alimentation pourra certainement répondre pendant un court instant).
En ce qui concerne le transistor 2N3055, celui-ci à un gain pour une température de 25°C et pour un courant de 8A (courant Ic) de G=20. Avec un gain de 20et un courant de collecteur de 8A on ce retrouve avec un courant de 0,4A !!!! dans ce cas notre petit circuit intégré NE555 va nous débiter un courant de 0,4A ?? (non je ne pense pas).
En regardant le Datasheets de ce dernier, celui-ci à des valeurs max à ne pas dépasse d’ailleur tension max = 18 V, nous sommes donc pile à la limite, ce qui est forcément risqué…
En ce qui concerne le courant de sortie de notre NE555 (Icc=10mA pour une tension de 15V maxi 15mA, mais je préfère rester en dessous.)
Prenons un courant de sortie de 10mA le transistor va donc avoir dans sa base un courant de 10mA qui va le parcourir, pour un courant de 10mA le courant Ic est proche de 1A, pour un courant de 12mA la chute de tension Vce est de l’ordre de 1,6V et la chute de tension Vbe=0,8V.
La résistance qui va venir limité le courant évitant la destruction de notre NE555 est de 1k4 normalisé 1k5 (15-0,8)/0.010=R2.
Bon il est vrai que pour un tel courant de base le transistor ne va pas amplifier grand-chose seulement un gain de 75 (valeur indiqué sur la courbe du datasheet).
Regardons en ce qui concerne la simulation, je place un générateur de 15V, et qui débite un courant de 1A, avec une chute de tension de 1,6V aux bornes du transistor 2N3055, et je met une résistance de 1k5 pour avoir un courant de 10mA.


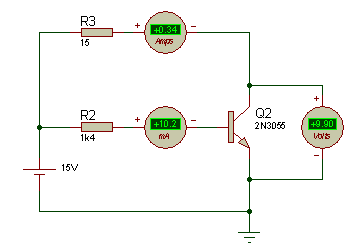
Tiens étonnant !! Aucune valeurs ne ressembles à mes calculs mise à part le courant Ib mais Vce et Ic??? Dequoi s’agit t’il ? est-ce une erreur de calcul (pourtant non), est-ce une erreur de lecture du datasheet (non) alors c’est quoi ?
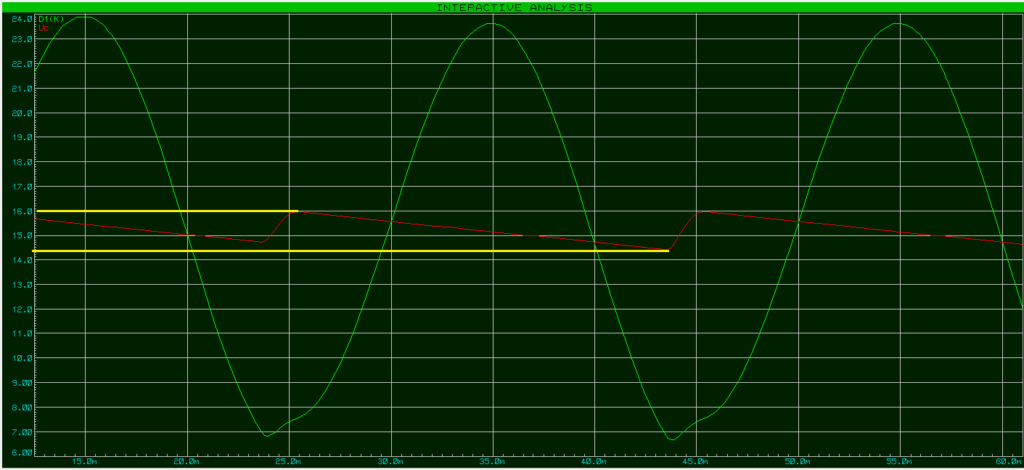
Ahhh mais oui !!!, voila l’erreur la fonction de transfert de notre 2N3055 par rapport à la simulation. J’ai fais une analyse de mon transistor 2N3055 grâce à l’outils interne à proteus. Quand on regarde le courant de base, et le courant collecteur en aucun cas ces résultats sont identiques avec le datasheet du 2N3055.
Regardons ensemble le courant Ic pour 1A, et le courant Ib :




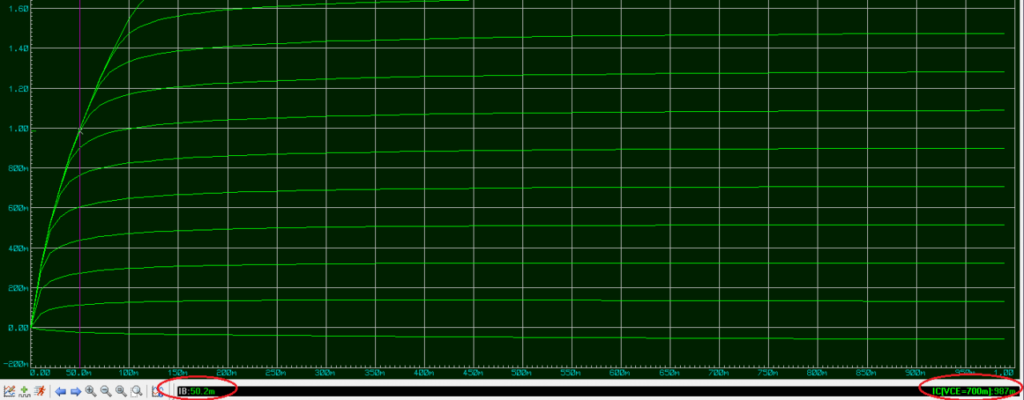
Pour un courant proche de 1A nous avons un Ib=50mA (environ) (différent de 10mA), alors la résistance R2 à donc une valeur de 284 Ohms (théorique) (15-0,8)/0.050=R2
Et pour un courant Ic=1A nous avons une chute de tension de 0,7V (différent de 1,6V)
Ic=(15-0,7)/1=14,3 Ohms (théorique) nous laisserons 15Ohms nous allons pas « chipoter » pour 0,7 Ohms…


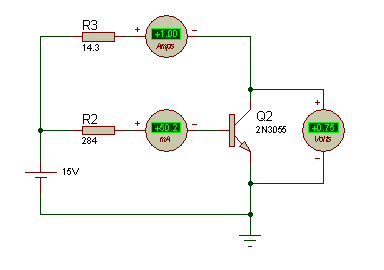
Alors ça par exemple !!!!
Mais une question alors, on se base sur quoi ? valeur théorique (logiciel) ou valeur pratique (datasheet), je vous laisses réfléchir…
(voir Théories fonction de transfert transistor NPN) pour les curieux…

Circuit imprimé

Historiques

23/09/2013
– 1er mise à disposition

Fonctionnement

Pour ceux qui ont lu ma page de calculs, il est évident que le potentiomètre RV1 a un rôle important dans ce montage filtre passe bas.

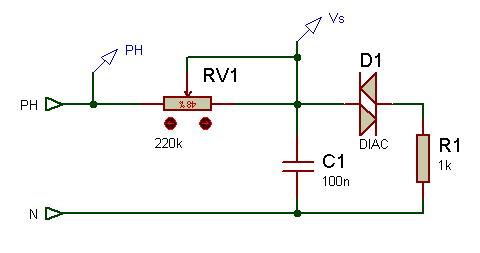
Ce qui est intéressant dans ce montage c’est que nos pouvons « jouer » sur la charge du condensateur, (retard à l’amorçage si on alimente un thyristor), On peut aussi assembler ce genre de montage avec un diac, comme ci-dessous.

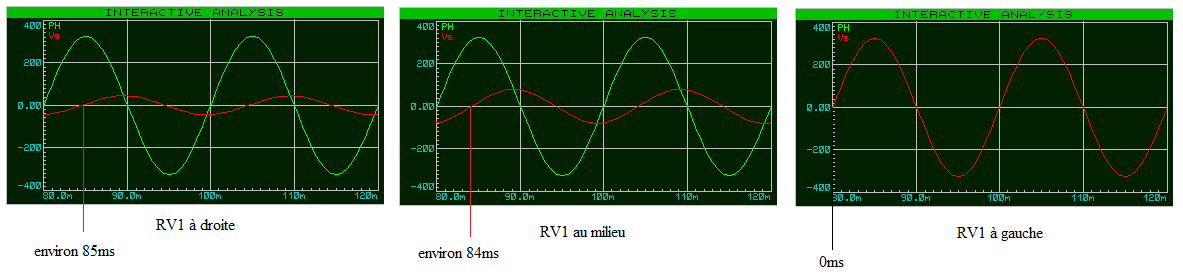
Potentiomètre RV1
Le principe est le suivant, lorsque le condensateur va se charger à travers RV1, le potentiel Vs (potentiel de sortie) sera retardé en fonction de l’angle, ainsi le zéro de la sinusoïde tension d’entrée Ve, et le zéro de la sinusoïde tension de sortie Vs est décalé. Le temps de charge du condensateur commencera à partir d’un certain temps, et en ce qui concerne le diac, qui deviens conducteur lorsque la tension dépasse un certain seuil (tension de retournement) va devenir passant entrainent la décharge brutal du condensateur C1.

Diac
Le diac est un composant qui est passant à une certaine tension (50V), et va venir amorcer le thyristor U1. En modifiant la valeur du potentiomètre RV1, nous modifions la temps de charge C1 ce qui va modifier l’amorçage de U1.

Dernière mise à jour le 30/01/2016

Filtre coupe passif du 2ème ordre

Ci-dessous un lien permettant de télécharger des documents techniques
– Choix du materiels

Dernière mise à jour le 25/01/2014

Présentation

Ce présent article permet de comprendre, de calculer et de voir comment se comporte un jeu de barre (tri ou mono) lorsque celui-ci se trouve confronté à un court-circuit. Je ne ferais pas un court magistral mais donné des notions pour le choix du ou des jeux de barres. Ils existent plusieurs techniques pour calculer un jeu de barre et plusieurs paramètres à pendre en compte, c’est pour cela que l’article qui suit est une ébauche sur le choix d’un jeu de barre.

Introduction

Le problème de la tenue aux efforts électrodynamiques se situe sur les circuits de puissance BT de l’installation. Elle est fonction principalement de l’intensité du courant de défaut mais aussi de la forme des conducteurs. Il peut être résolu par calcul. Mais seule la validation par un essai grandeur réelle permet de fournir un document reconnaissant la conformité aux exigences normatives. Les intensités très élevées qui peuvent apparaître lors d’un court-circuit entre les différents conducteurs d’une installation BT (conducteurs massifs du type barres, câbles…) engendrent des efforts considérables (plusieurs milliers de daN par mètre).Leur détermination est donc nécessaire afin de dimensionner mécaniquement. les conducteurs eux-mêmes et les structures qui les supportent pour qu’ils résistent à de tels efforts quelles que soient les protections placées en amont et en aval (les normes demandent des essais de tenue électrodynamique d’une durée d’une seconde). Le calcul exact des efforts électrodynamiques est souvent complexe compte tenue de la géométrie des conducteurs et des structures associées.

Disposition du conducteur
Pour transporté de fortes intensités, en courant alternatif, il n’est pas possible d’utiliser un conducteur unique, qu’il soit plein, méplat, ou rond. En effet, la self induction réduit la section utile offerte au passage du courant à une « peau » qui rend illusoire l’augmentation des dimensions.

Pourquoi le jeu de barre va se tordre en fonction du courant de court-circuit (kA)
Pour examiner de plus près ce phénomène, il faut étudier un point situé sur le jeu de barre, et désolé mais les mathématiques vont apparaitre encore une fois.

Champ magnétique cree par un courant

Loi de Biot et Savart.Les physiciens français Biot et Savart ont trouvé l’expression du champ magnétique.Un fil conducteur rectiligne de longueur infinie, parcouru par un courant I , crée, en un point M de l’espace situé à une distance r du fil, un champ magnétique dont :
– la direction est telle que les lignes de champ soient des cercles axés sur le fil.
– le sens est donné par la règle du ″bonhomme d’Ampère″: celui-ci, lorsqu’il est parcouru par I , des pieds vers la tête, voit en M le champ à sa gauche.

Ce qu’il faut retenir c’est que la formule de Biot et Savart donne la valeur du champ magnétique part :
B=(µ0*I)/(2*3,14*R)
B : Champ magnétique
µ0 : μ0 est la perméabilité magnétique du vide C’est une constante universelle
μ0=4p×10-7 H/m.
R : la distance du point du champ (si nous voulons le calculer) par rapport au fil.

Direction des lignes de champs lorsque deux conducteurs sont en parallèles


Pas super le dessin mais cela donne une idée…
Deux conducteurs en parallèles (ou deux jeux de barres) formes des lignes de champs entres ces deux jeux de barres. La direction de ces lignes de champs dépend du sens du courant (les deux courants situés vers le haut), et si ce courant est dans le même sens alors nos avons pour le jeu de barre qui est situé à gauche une ligne de champs qui donne une face Nord et pour le jeu de barre qui est situé à droite donne une face sud. En effet si on analyse le sens du champ magnétique du jeu de barre situé à gauche, on peut représenter un « N » comme Nord et pour le jeu de barre situé à droite on peut représenter un « S » comme Sud.
Cette petite analyse donne naissance à deux pôles qui s’attirent lorsque ils ne sont pas du même nom, et il en résulte que ces deux jeu de barre vont théoriquement s’attirer comme le montre les flèches rouge).
Si les courants avaient été dans le sens inverse alors nous obtenons des pôle de même nom et il en résulte que dans ce cas les barres se repoussent.

Exemple1

Prenons pour exemple deux jeux de barres qui sont parcourus par le même courant, et prenons un courant de court-circuit de 30kA avec une distance entre ces barres de 50cm sur une longueur de 5m.
A partir de la loi de Laplace et de la loi de Biot et Savart, on montre que les deux fils s’attirent avec une force d’intensité :
F1=F2=BIL=(µ0*I)/(2*3,14*R)*L (F=BIL si l’angle égale 90° sin 90°=1)
Ainsi si on mélange Laplace F=B*I*L* sin (x) puis Biot et Savart nous obtenons une force de
F1=F2=(4*3,14*10^-7*30000)/(2*3,14*0,05)*5=0,6N => soit environ 6 Kg

Puis pour une longueur de 10m
F1=F2=(4*3,14*10^-7*30000)/(2*3,14*0,05)*10=1,2N=> soit environ 10 Kg
Le rayon de courbure de ces deux jeux de barres pourrait bien venir s’embrasser et avoir le coup de foudre …

Méthode par abaque


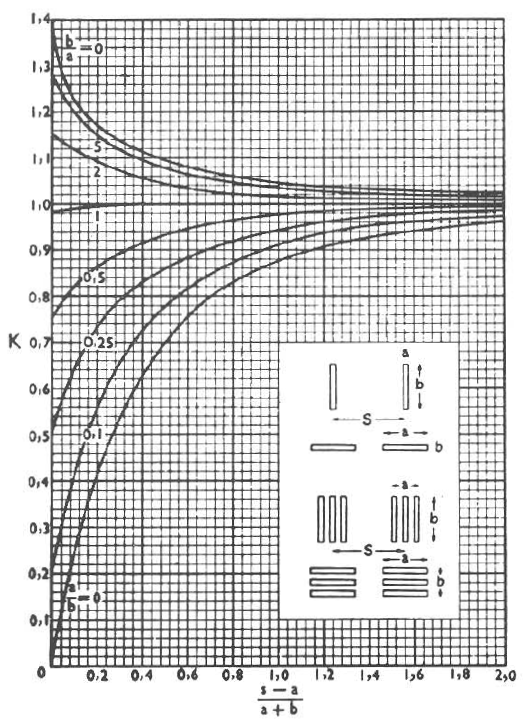
(clique pour agrandir)
Bien entendu les calculs donnés précédemment donne une vison de ce qu’il pourrait se passer, une méthode plus rigoureuse est l’utilisation d’une courbe (comme celle situé ci-dessus). Nous pouvons cependant calculer l’effort maximum en courant continu et en monophasé par la relation suivante :
Fmax = 2,04*I1*I2*(L/s)*10^-8
Avec
Fmax : Force maximal en Kg
I1 et I2 : courant en Apmères
L : longueur des conducteurs en cm entre support (ou cales)
s : distances séparant les conducteurs en cm.

Puis en court-circuit :
I1 = I2 = I (I représente bien entendu la valeur maximum que peut prendre le courant de court-circuit)
Fmax = 2,04*I²*(L/s)*10^-8
 

 

Facteur de forme
La formule précédente ne s’applique qu’à des conducteurs ronds. Lorsqu’il s s’agit de matériaux plats, il est nécessaire d’introduire un facteur de correction K dans la formule, sauf si les conducteurs sont très petit ou très éloignés (Dwight).
On a alors :
Fmax= 2,04*I²*(L/s)*K*10¨-8La courbe précendete donne K en fonction de l’expression (s-a)/(a+b) pour différentes valeurs de (a/b) ; « a » représentant l’épaisseur de la barre ou du groupes de barres, « b » la hauteur de la barre ou du groupes de barres, et « s » l’entraxe des barres ou groupes de barres.

Exemple 2

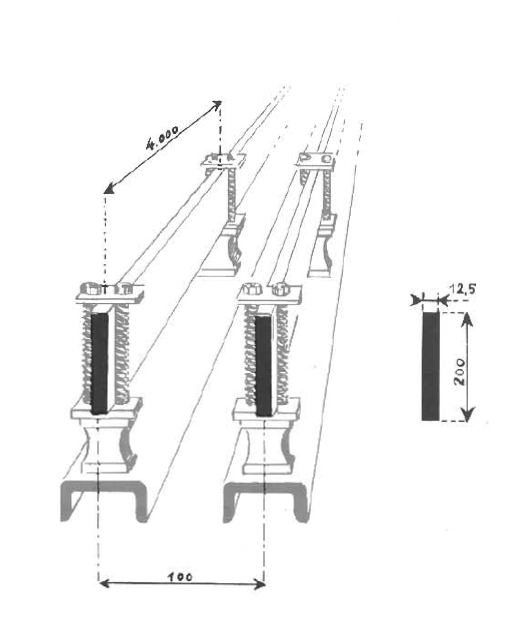
Effort s’exerçant en cas de court-circuit monophasé sur une portée entre deux barres de 200*12,5mm écartées de 100mm. Longueur de la portée : 4m
Courant de court-circuit I=30kA

Détermination de K :
a=1,25cm ;
b=20cm ;
s=10cm.
a/b=1,25/20=0,06
(s-a)/(a+b)=8,75/21,25=0,41
K=0,68 (environ)
L/s=400/10=40
Pour un court-circuit monophasé la figure 3 donne la valeur de la force unitaire noté F, on peut relevé pour I=30kA F=18,4Kg
D’où Fmax=18,4*40*0,68=500kG !! (environ).

Grâce à cette valeur nous pouvons déterminer le support des isolateurs, en calculant le moment de flexion c’est ce que nous allons voir juste en dessous ;-).

Moment de flexion résultant

Nous avons trouver Fmax, il faut mainenant trouver le moment de flexion résultant soit M avec :

M=(F*L²)/k
L : distance entre appuis
k : coefficient dépendant du mode de fixation (8 pour les appuis simple et 12 pour les encastrement).
À vous de jouer maintenant 😉

Ci-dessous un lien permettant de télécharger des documents techniques
– Eclairagisme 1

Dernière mise à jour le 28/03/2014

Dynamique des fluides c’est quoi?

Je vous laisse lire Notions mecanique des fluides

Dernière mise à jour le 12/04/2014

Présentation

Il est parfois nécessaire de se munir de doubleur de tension quand justement, la tension au niveau du transformateur est faible. Ils ne peuvent pas fonctionner à partir d’une tension continue, et il faut dans ce cas transformer la tension continue en une tension alternative. Le but de ce présent article est de calculer les composants nécessaires pour subvenir à vos besoins. En utilisant seulement deux condensateurs et deux diodes nous avons un doubleur de tension, retse à savoir comment les placer et comment les déterminés c’est le but de l’article.

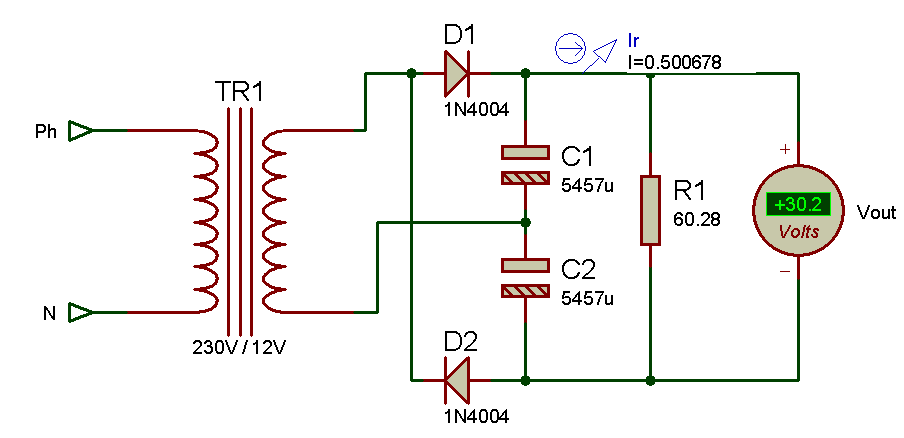
Doubleur de tension de Latour

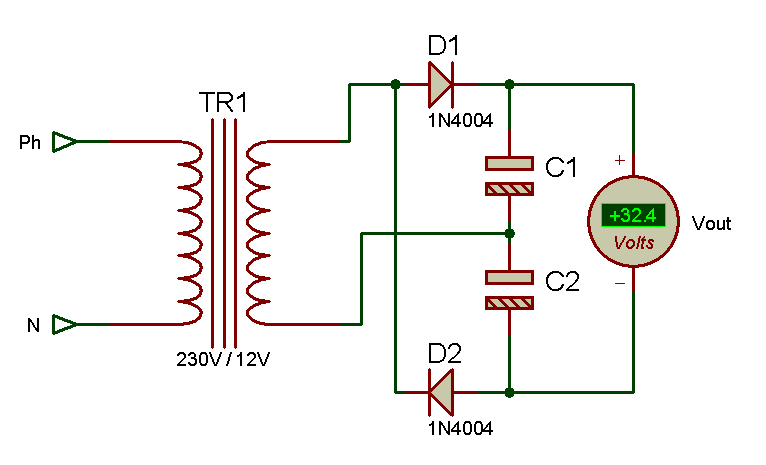
Fonctionnement
Le fonctionnement est le suivant, à la première alternance la tension est positive sur l’anode de D1, et cette même diode devient passante avec une chute de tension d’environ 0,6V, le condensateur étant connecté entre le potentiel positive et le « retour » celui-ci se charge sur la première alternance. Au moment ou l’alternance positive atteint son maximum bien évidement elle diminue, mais le condensateur C1 lui rets chargé à la tension maxi soit 12*racine carré de 2 qui est d’environ 17V (pararrondi). Au moment ou la tension devient nul, et passe au potentiel négatif, c’est la diode D2 qui prend le relais et devient passante, ainsi au tour du condensateur C2 de se charge jusqu’à la tension maxi qui est de -12*racine carré de 2=-17V (tension négative), si on place un voltmètre en sortie de ce doubleur de tension nous obtenons Vout=17-(-17)=34V. Or sachant que la chute de tension des diodes est d’environ 0,6V nous obtenons Vout=34-(0,6+0,6)=34-1,2=32,8V, théorique.

Choix du condensateur
Le condensateur doit pouvoir maintenir une tension crête soit la tension de l’alimentation qui est d’environ 17V. un condensateur de 16V suffit avec les tolérance tous rentre dans l’ordre mais si l’alimentation est supérieur à 12V il serais plus judicieux d’élever la valeur du condensateur.
Courant et tension

Prenons le cas ou une charge serait connectée en sortie et qui celle-ci consomme un courant de500mA, il faudrait dimensionner correctement le condensateur pour que celui-ci donne un peu de pêche à notre montage lorsque la tension est inférieure à la tension emmagasiné par notre condensateur, oui vous avez compris le condensateur doit prendre le relais et fournir le courant au moment de sa décharge. Toujours en prenant le même exemple avec une alimentation de 12V on désire avoir un taux d’ondulation* de 10%, ce qui donne une valeur Max=17V et une valeur Min=15,27V. La valeur moyenne ce situe entre ces deux valeur soit 16,27V.
Ic=C*du/dt => C=(Ic*dt)/du, et oui !! Encore de retour. Il faut se baser par rapport à la tension qui se situe sur le condensateur, le condensateur C1 voit une tension qui correspond uniquement à la 1ère alternance, et la 2ème alternance est assurée par C2. Il en résulte que les condensateurs C1 et C2 voient une sur deux une alternance, la période est donc de 50Hz.
C=(Ic*dt)/du=(0,5*0,0185)/(17-15,27)=5346µF (théorique), si on ajoute une charge qui consomme un courant de 500mA sachant que la chute de tension dans les diodes est de 0,6V on doit avoir une tension aux bornes de cette charge de 30,14V (toujours théorique). La résistance doit être de R1=30,14/0,5=60,28Ohms (théorique encore une fois).
Les résultats sont proches de la théorie, et on retrouve bien Umax =17V (imprécisions des mesures) Umin=15V.

Taux=(Umax-Umini)/Umoyen

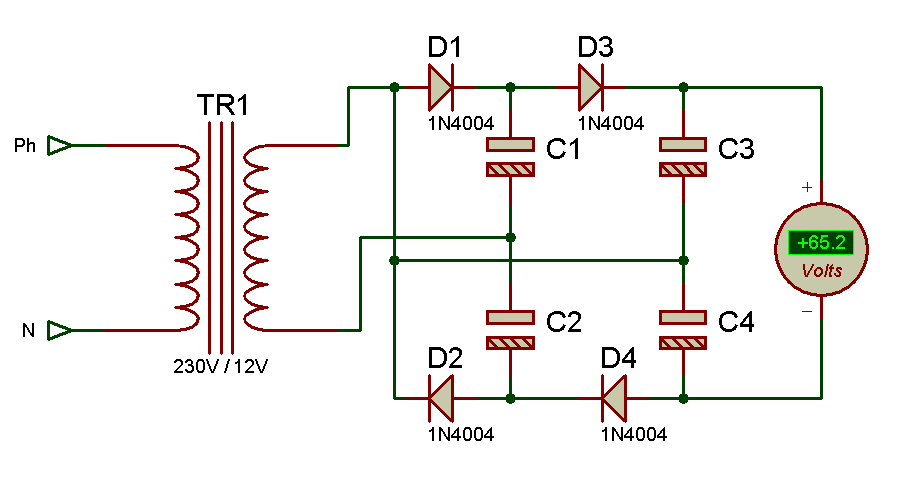
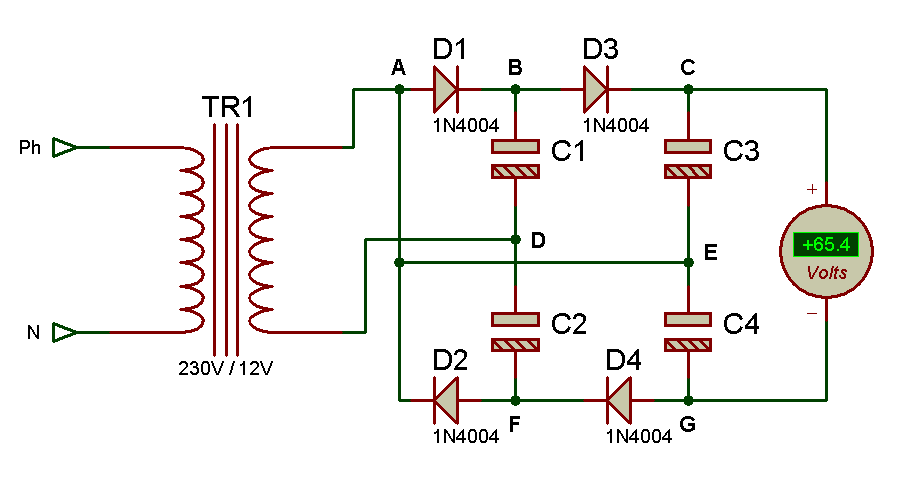
Quadrupleur de tension de Latour

Interessons nous maintenant à un autre type de montage. Comme son nom l’indique ce montage permet de multiplier par 4 fois la tension d’entrée.
Fonctionnement

Prenons le montage à la mise sous tension, tous les condensateurs sont déchargés, je ne vais pas faire une démonstration de calculs, mais de montrer comment la tension évolue dans le temps. Pour la première alternance positive, la diode D1 est passante, et la tension du réseau évolue jusqu’à la valeur crête soit 12*racine carré de 2=17V (environ), le condensateur C1 se charge et le potentiel A est égale à la tension crête du réseau (si on néglige la chute de tension de la diode D1), on retrouve la valeur max soit 17V à ses bornes (effectivement l’autre extrémité, plus précisément la patte du condensateur est relié au point de référence « 0V »). Le condensateur C1 étant chargé, on retrouve la tension (moins la chute de tension de la diode D3) au potentiel C à un potentiel de d’environ 16,4V. Au moment ou la tension est inférieure au potentiel B (potentiel maintenu fixe grâce au condensateur C1), la diode est bloquée puis plus cette tension diminue plus la tension aux bornes de C3 augmente (bien évidement le potentiel C reste fixe tant que le condensateur ne se décharge pas) ainsi lorsque la tension au potentiel E=A arrive dans l’alternance négative et arrive à la valeur -17V, la diode D2 est passante et le réseau impose sa tension, le condensateur C2 se charge à une tension de -17V, ce qui entraine à rendre passant la diode D4 et ce qui impose -17V au potentiel G (à condition que le condensateur ne se décharge pas).
De retour à l’alternance positive et de retour à la valeur crête le potentiel B inchangé ainsi que le potentiel C, en revanche le potentiel E lui varie entre -17V et +17V, puis les potentiels F et G sont inchangés aussi, et ont des valeurs négative (-17V). Lorsque le potentiel E est situé à +17V la tension aux borne du condensateur C4 est de Veg=Ve-Vg=+17-(-17)=34V. puis lorsque le potentiel E se situe à -17V la tension aux bornes de C3 est de Vce=Vc-Ve=17-(-17)=34V ce qui donne une tension Vcg=34V+34V=68V.
Si on souhaite être à la virgule, il suffit de faire Vout=Vcg=4*12*racine carré de 2-(0,6*4)=65,482V, c’est d’ailleurs ce qu’on obtient en simulation.
Il en résulte que les condensateur C1 et C2 ont une tension de 12*racine carré de 2 moins la chute de tension de la diode (0,6V)= 16,3V,puis pour les condensateurs C3 et C4 la tension est de 2*12*racine carré de 2-(2*0,6V puisque il y’a les deux diodes précédentes en série)=32,7V.

Choix du condensateur
Pour les condensateurs C1 et C2 16V suffit, en ce qui concerne C3 et C4 il suffit de multiplier par deux la tension de service 35V est suffisant, oui!! puisque la tension aux bornes du condensateur est deux fois plus importante que les deux premiers, et si on décide de faire un montage en cascade elle sera encore 4 fois plus importante./span>

Courant et tension
On se basera sur le même calcul évoqué précédement.

Historiques

12/04/2014
– 1er mise à disposition

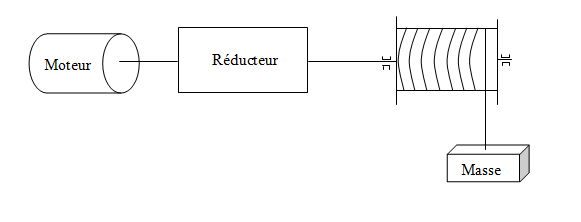
Dimensionnement d’un système d’entraînement

Partie 1

Caractéristiques des appareils :
– treuil diamètre du tambour d = 20 cm, h = 0,9
– réducteur : rapport de réduction = 60, h = 0,85
– moteur : vitesse de rotation en charge = 1450 min-‘, h = 0,85,
– diamètre de l’axe d = 20 mm.

1 – Calculer le travail utile effectué (g = 9,81).
2 – Calculer la puissance utile.
3 – Calculer le travail fourni par l’axe du moteur.
4 – Calculer la puissance mécanique fournie par le moteur.
5 – Calculer le total d’énergie consommée et la puissance totale nécessaire.
6 – Calculer la vitesse angulaire du tambour du treuil et le couple correspondant à la force motrice.
7 – Calculer le couple -ramené sur l’axe moteur et la force exercée par le moteur sur l’axe du réducteur.

Partie 2 (même exemple mais changement des valeurs)

Un système de levage est composé :
– D’un moteur, de moment d’inertie Jm = 0,008 kg.m2 qui tourne à la vitesse n = 1 450 tr/min.
– D’un réducteur, de rapport (6/145), et de moment d’inertie négligeable.
– D’un cylindre en rotation qui tourne à la vitesse n’ = 60 tr/mn et dont l’inertie Jc = 2,4 kg.m2.
– D’une masse de 200 kg se déplaçant linéairement à 1,2 m/s.
– Le couple résistant de la charge est de 150 N.m à la vitesse de rotation n’ = 60 tr/min.
– Le moteur d’entraînement a un couple moyen au démarrage de 12 N.m.

1 – Calculer la. vitesse angulaire du moteur.
2 – Calculer le moment d’inertie total du système, ramené à la fréquence de rotation du moteur.
Rappel : Le moment d’inertie d’une charge tournant à la vitesse n2 ou w2 ramenée à la vitesse n1 ou w1, du moteur est : Js = Je(n2/n1)2 = Je(w2 / wI)2.
I’inertie d’une masse M en mouvement linéaire à la vitesse v ramenée à la vitesse w du moteur est : Js = M(v/w)2.
3 – Calculer le couple résistant ramené à la vitesse du moteur.
4 – Calculer le couple d’accélération (différence entre le couple de démarrage et le couple résistant).
5 – Calculer le temps de démarrage.
6 – Admettons que nous voulions limiter le temps de démarrage à 0,5 s.. Quel devrait être, dans ce cas, le couple moyen de démarrage du moteur ?
7 – Pour une raison quelconque, il y a rupture de la liaison entre le réducteur et le cylindre, la masse «tombe» à la vitesse de 0,5 m/s. Afm d’assurer la sécurité, on a prévu un frein mécanique capable d’arrêter la masse après 1 m de chute.
8 – Calculer l’énergie et la puissance dissipée sous forme de chaleur par le frein, pour stopper la charge en 4 s. On supposera que le mouvement est uniformément varié et on ne tiendra compte que de l’inertie de la masse.

Correction partie 1

1 – Travail utile effectué :
W = F.L, dans ce cas F correspond au poids de la charge, soit M.g = 100 x 9,81 et L au déplacement L = 10 m.
Wu = Mgh = 100 x 9,81 x 10 = 9 810 J.

2 – Puissance utile :
PU = Wu/t : nous venons de calculer Wu, il faut déterminer t :
Nombre de tours de tambour nécessaire pour élever la charge de 10 m : 10/pd = 10/(0,2.pi) = 16 tours.
– Temps mis pour faire un tour de tambour =>(60/1 450) x 60 = 2,5 s.
– Temps mis pour effectuer le travail =>2,5 x 16 = 40 s.
Pu = Wu/t = 9 810/40 = 245,25 W

3 – Travail fourni par l’axe du moteur :
– Attention, les rendements se multiplient
ht x hr = 0,9 x 0,85 = 0,765
Wu = 9 810/0,765 = 12 823,5 J.

4 – Puissance mécanique fournie par le moteur :
12 823,5/40 = 320,6 W. (Le travail a été effectué en 40 s).

5 – Total de l’énergie consommée :
– Il faut tenir compte du rendement du moteur => 12 823,5/0,85 = 15 086,5 J.
– Puissance nécessaire => 15 086,5/40 = 377 W.
Vérification :
245,25/(0,9.0,85.0,85)= 377 W.

6 – Vitesse angulaire du treuil et couple :
w = 2p/n = 6,28/2,5 = 2,5 rad/s.
C = (Pu/w) = 245,25/2,5 = 98,1 N.m.

7 – Couple ramené sur l’axe du moteur :
– Avec un réducteur, ce que l’on gagne en vitesse on le perd en couple. La vitesse côté moteur a augmenté de 60, le couple diminue donc de 60, sans oublier le rendement soit : 98,1/(0,9.0,85.60) = 2,13 N.m.
Vérifications avec le moteur:
Cm=(Pm/wm)=(320,6/(2.pi.(1450/60))=2,111N.m (différent de 2,13N.m. pourquoi (les arrondis))
Remarques: je vais refaire le calcul pour être encore plus précis à cause ce ces arrondis nous sommes pas à la virgule près….
 

 

Pour les tours du treuil1tr de treuil => 2.pi.r(rayon)
10tr de treuil => 10/(2.pi.r)=15,9154.. tours et non 16 trs(1er arrondi)

En ce qui concerne le temps en (s)
Nm(moteur)=1450/60 tr/s Nt(treuil)=((1450/60)/60) tr/s
10/(2.pi.r)/Nt=10/(2.pi.0,1)/((1450/60)/60)=39,514… sec et non 40sec (2éme arrondis)
La puissance utile
Pu=Wu/t=(9810/(10/(2.pi.0,1)/((1450/60)/60))=248,26…W et non 245,25W (3éme arrondis)
Puissance mécanique fournie par le moteur
Pm=Pu/(ht.hr)=(10/(2.pi.0,1)/((1450/60)/60))/(0,9.0,85)=324,264…W et non 320,58W (4éme arrondis)
Le couple moteur est donc :
Cm=Pm/wm=(10/(2.pi.0,1)/((1450/60)/60))/(0,9.0,85)/((1450/60).2.pi))=2,137254 N.m (enfin c’est juste !!!)
Force exercée sur l’axe du réducteur par le moteur:
2,13/0,01 = 213 N.

Correction partie 2

1 – Vitesse angulaire du moteur :
w = 2pn/60 = 6,28 x 1 450/60 = 152 rad/s.

2 – Moment d’inertie total du système :
Lorsque dans un système d’entraînement, des masses tournent à des vitesses différentes, ou se déplacent en mouvement linëaire, il faut ramener leur moment d’inertie à la fréquence de rotation du moteur.
Inertie du moteur =>Jm = 0,008 kg.m2
Inertie du cylindre en rotation, ramenée au moteur => Jc = 2,4 x (60/1 450)2 = 0,0041 kg.m 2
Inertie de la masse se déplaçant linéairement, ramenée au moteur => Jm = 200 x (1,2/152)2 = 0,0125 kg.m 2 .
Jt = 0,008 + 0,0041 + 0,0125
Jt = 0,0246 kg.m2 .

3 – Couple résistant ramené à la vitesse du moteur :
Cr = 150 x 60/1 450 = 6,2 N.m.

4 – Couple d’accélération :
Ca = 12 – 6,2 = 5,8 N.m.

5 – Temps de démarrage :
Ca = Jw = J(dw)/dt
dt = J(dw)/Ca
dt = 0,0246 x 152/5,8 = 0,64 s.

6 – Couple d’accélération :
Ca = J(dw/dt)
Ca = 0,0246 x (152/0,5) = 7,48 N.m.
Couple moyen de démarrage du moteur:
7,48 + 6,2 = 13,68 N.m.

7. Énergie dissipée par le frein :
Wfrein = Mgh + 1/2 MV2
Mgh = 200 x 9,81 x 1 = 1962 J
1/2MV2 = 1/2 x 200 X 0,52 = 25 J
Wfrein = 1 962 + 25 = 1 987 J
Puissance dissipée sous forme de chaleur:
P = W/t = 1 987/4 = 496,76 W

Ci-dessous un lien permettant de télécharger des documents techniques
– Cours électromecanique