Dernière mise à jour le 25/01/2014
Présentation
Ce présent article permet de comprendre, de calculer et de voir comment se comporte un jeu de barre (tri ou mono) lorsque celui-ci se trouve confronté à un court-circuit. Je ne ferais pas un court magistral mais donné des notions pour le choix du ou des jeux de barres. Ils existent plusieurs techniques pour calculer un jeu de barre et plusieurs paramètres à pendre en compte, c’est pour cela que l’article qui suit est une ébauche sur le choix d’un jeu de barre.
Introduction
Le problème de la tenue aux efforts électrodynamiques se situe sur les circuits de puissance BT de l’installation. Elle est fonction principalement de l’intensité du courant de défaut mais aussi de la forme des conducteurs. Il peut être résolu par calcul. Mais seule la validation par un essai grandeur réelle permet de fournir un document reconnaissant la conformité aux exigences normatives. Les intensités très élevées qui peuvent apparaître lors d’un court-circuit entre les différents conducteurs d’une installation BT (conducteurs massifs du type barres, câbles…) engendrent des efforts considérables (plusieurs milliers de daN par mètre).Leur détermination est donc nécessaire afin de dimensionner mécaniquement. les conducteurs eux-mêmes et les structures qui les supportent pour qu’ils résistent à de tels efforts quelles que soient les protections placées en amont et en aval (les normes demandent des essais de tenue électrodynamique d’une durée d’une seconde). Le calcul exact des efforts électrodynamiques est souvent complexe compte tenue de la géométrie des conducteurs et des structures associées.
Disposition du conducteur
Pour transporté de fortes intensités, en courant alternatif, il n’est pas possible d’utiliser un conducteur unique, qu’il soit plein, méplat, ou rond. En effet, la self induction réduit la section utile offerte au passage du courant à une « peau » qui rend illusoire l’augmentation des dimensions.
Pourquoi le jeu de barre va se tordre en fonction du courant de court-circuit (kA)
Pour examiner de plus près ce phénomène, il faut étudier un point situé sur le jeu de barre, et désolé mais les mathématiques vont apparaitre encore une fois.
Champ magnétique cree par un courant
Loi de Biot et Savart.Les physiciens français Biot et Savart ont trouvé l’expression du champ magnétique.Un fil conducteur rectiligne de longueur infinie, parcouru par un courant I , crée, en un point M de l’espace situé à une distance r du fil, un champ magnétique dont :
– la direction est telle que les lignes de champ soient des cercles axés sur le fil.
– le sens est donné par la règle du ″bonhomme d’Ampère″: celui-ci, lorsqu’il est parcouru par I , des pieds vers la tête, voit en M le champ à sa gauche.
Ce qu’il faut retenir c’est que la formule de Biot et Savart donne la valeur du champ magnétique part :
B=(µ0*I)/(2*3,14*R)
B : Champ magnétique
µ0 : μ0 est la perméabilité magnétique du vide C’est une constante universelle
μ0=4p×10-7 H/m.
R : la distance du point du champ (si nous voulons le calculer) par rapport au fil.
Direction des lignes de champs lorsque deux conducteurs sont en parallèles

Pas super le dessin mais cela donne une idée…
Deux conducteurs en parallèles (ou deux jeux de barres) formes des lignes de champs entres ces deux jeux de barres. La direction de ces lignes de champs dépend du sens du courant (les deux courants situés vers le haut), et si ce courant est dans le même sens alors nos avons pour le jeu de barre qui est situé à gauche une ligne de champs qui donne une face Nord et pour le jeu de barre qui est situé à droite donne une face sud. En effet si on analyse le sens du champ magnétique du jeu de barre situé à gauche, on peut représenter un « N » comme Nord et pour le jeu de barre situé à droite on peut représenter un « S » comme Sud.
Cette petite analyse donne naissance à deux pôles qui s’attirent lorsque ils ne sont pas du même nom, et il en résulte que ces deux jeu de barre vont théoriquement s’attirer comme le montre les flèches rouge).
Si les courants avaient été dans le sens inverse alors nous obtenons des pôle de même nom et il en résulte que dans ce cas les barres se repoussent.
Exemple1
Prenons pour exemple deux jeux de barres qui sont parcourus par le même courant, et prenons un courant de court-circuit de 30kA avec une distance entre ces barres de 50cm sur une longueur de 5m.
A partir de la loi de Laplace et de la loi de Biot et Savart, on montre que les deux fils s’attirent avec une force d’intensité :
F1=F2=BIL=(µ0*I)/(2*3,14*R)*L (F=BIL si l’angle égale 90° sin 90°=1)
Ainsi si on mélange Laplace F=B*I*L* sin (x) puis Biot et Savart nous obtenons une force de
F1=F2=(4*3,14*10^-7*30000)/(2*3,14*0,05)*5=0,6N => soit environ 6 Kg
Puis pour une longueur de 10m
F1=F2=(4*3,14*10^-7*30000)/(2*3,14*0,05)*10=1,2N=> soit environ 10 Kg
Le rayon de courbure de ces deux jeux de barres pourrait bien venir s’embrasser et avoir le coup de foudre …
Méthode par abaque
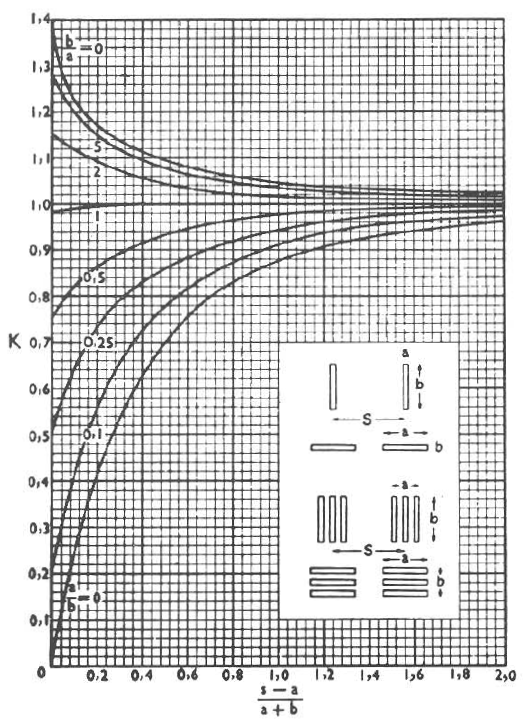
(clique pour agrandir)
Bien entendu les calculs donnés précédemment donne une vison de ce qu’il pourrait se passer, une méthode plus rigoureuse est l’utilisation d’une courbe (comme celle situé ci-dessus). Nous pouvons cependant calculer l’effort maximum en courant continu et en monophasé par la relation suivante :
Fmax = 2,04*I1*I2*(L/s)*10^-8
Avec
Fmax : Force maximal en Kg
I1 et I2 : courant en Apmères
L : longueur des conducteurs en cm entre support (ou cales)
s : distances séparant les conducteurs en cm.
Puis en court-circuit :
I1 = I2 = I (I représente bien entendu la valeur maximum que peut prendre le courant de court-circuit)
Fmax = 2,04*I²*(L/s)*10^-8
Facteur de forme
La formule précédente ne s’applique qu’à des conducteurs ronds. Lorsqu’il s s’agit de matériaux plats, il est nécessaire d’introduire un facteur de correction K dans la formule, sauf si les conducteurs sont très petit ou très éloignés (Dwight).
On a alors :
Fmax= 2,04*I²*(L/s)*K*10¨-8La courbe précendete donne K en fonction de l’expression (s-a)/(a+b) pour différentes valeurs de (a/b) ; « a » représentant l’épaisseur de la barre ou du groupes de barres, « b » la hauteur de la barre ou du groupes de barres, et « s » l’entraxe des barres ou groupes de barres.
Exemple 2
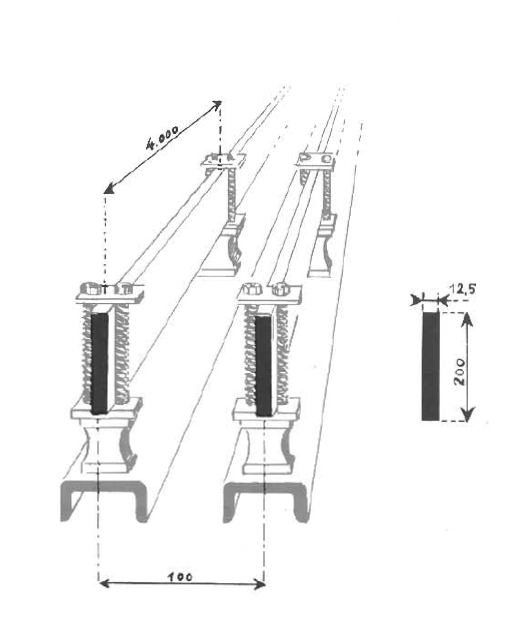
Effort s’exerçant en cas de court-circuit monophasé sur une portée entre deux barres de 200*12,5mm écartées de 100mm. Longueur de la portée : 4m
Courant de court-circuit I=30kA
Détermination de K :
a=1,25cm ;
b=20cm ;
s=10cm.
a/b=1,25/20=0,06
(s-a)/(a+b)=8,75/21,25=0,41
K=0,68 (environ)
L/s=400/10=40
Pour un court-circuit monophasé la figure 3 donne la valeur de la force unitaire noté F, on peut relevé pour I=30kA F=18,4Kg
D’où Fmax=18,4*40*0,68=500kG !! (environ).
Grâce à cette valeur nous pouvons déterminer le support des isolateurs, en calculant le moment de flexion c’est ce que nous allons voir juste en dessous ;-).
Moment de flexion résultant
Nous avons trouver Fmax, il faut mainenant trouver le moment de flexion résultant soit M avec :
M=(F*L²)/k
L : distance entre appuis
k : coefficient dépendant du mode de fixation (8 pour les appuis simple et 12 pour les encastrement).
À vous de jouer maintenant 😉