Monthly Archives: February 2016
Condensateur de démarrage
Voir aussi => Moteur asynchrone monophasé
Les condensateurs de démarrage: possèdent une importante capacité pouvant dépasser les 100 microfarads. Ils doivent absolument pas resté sous tension sinon ils s’échauffent très rapidement et risquent d’exploser. (un contact centrifuge va venir s’ouvrir et ainsi déconnecter le condensateur de démarrage)
Moteur à 4 fils de sorties et contact centrifuge incorporé au moteur, 2 sens de rotation:
Représentation avec plaque à bornes:
Plaques à bornes commercialisées

Montage à 4 fils avec 2 sens de rotation avec barrettes de connexions (sur plaque à bornes):
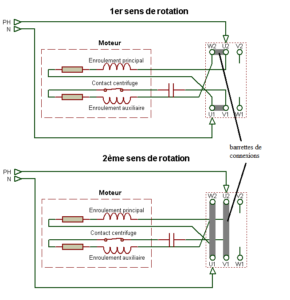
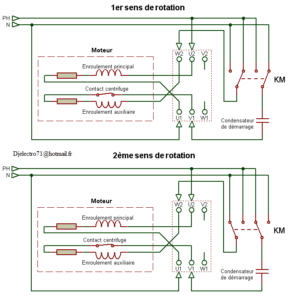
Montage à 4 fils avec 2 sens de rotation par contacteur de ligne (sur plaque à bornes):
les fils du moteur sont relié à chaque pattes de la plaque à bornes en respectant U1/V1/U2/W2.
Dans cette configuration les barrettes sont remplacées par un contacteur de ligne, ce qui permettra d’éviter de changer à chaque fois les barrettes de places…
L’enroulement Principale ou enroulement de marche (run) est constitué d’un gros fil prévu pour resté en permanence sous tension. L’enroulement Auxiliaire ou enroulement de démarrage (start) est constitué d’un fil plus fin il est prévu pour permettre le démarrage du moteur. Si l’enroulement de démarrage n’est pas raccordé le moteur ne peut pas démarrer sauf si il est lancé a la main.
Moteur à 6 fils de sorties et contact centrifuge incorporé au moteur, 2 sens de rotation
la différence avec le schéma précédent est que les 2 fils du contact centrifuge sont sortis.
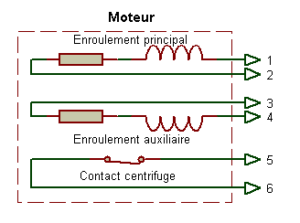
Montage à 6 fils avec 2 sens de rotation avec barrettes de connexions (sur plaque à bornes):
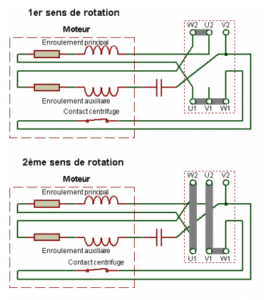
Je n’est pas mis l’alimentation pour qu’on remarque que celle-ci ce fais toujours sur U1 et U2
Montage à 6 fils avec 2 sens de rotation par contacteur de ligne (sur plaque à bornes):
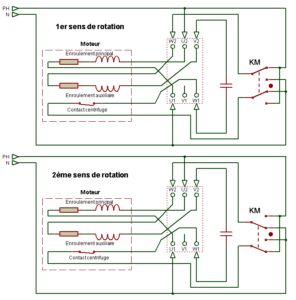
Montage à 4 fils avec 2 sens de rotation et relais d’intensité (sur plaque à bornes):
Le fonctionnement du relais d’intensité comme son nom l’indique varie en fonction de l’intensité, la forte intensité due au démarrage traverse l’enroulement permanent et génère un flux magnétique suffisant pour coller le contact et alimenter l’enroulement de démarrage. Lorsque le moteur est lancé et dès qu’il prend de la vitesse, l’appel d’intensité diminue, la force du champ magnétique de la bobine du relais diminue et le contact s’ouvre, l’enroulement de démarrage (enroulement auxiliaire) n’est plus alimenté, et le moteur continu à tourner avec l’enroulement principale (ou permanent).
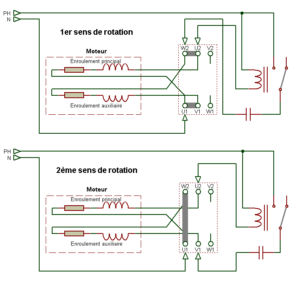
Montage à 4 fils avec 2 sens de rotations et relais d’intensité avec contacteur de ligne (sur plaque à borne):
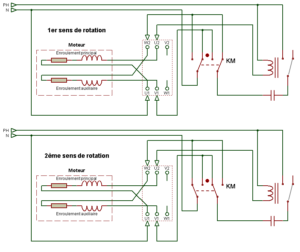
Fonctionnement du condensateur de démarrage
Un moteur asynchrone monophasé ne peut démarrer tout seul, faute de déphasage entre l’inducteur et l’induit (donc de couple) en absence de condensateur de démarrage. Nous verrons plus loin sont rôle. Il faut savoir qu’il est tous à fais possible de faire tourner un moteur asynchrone monophasé si on le lance à la main, ainsi le sens de rotation sera attribué dans le sens ou nous avons fais tourné le moteur.
Calculs du condensateur de démarrage
Une formule à retenir rien qu’une!!
C=50xPx(220:U)²x(50:F)
C = condensateur en uF
P= Puissance en Chevaux (1 CV = 736W)
U = Tension
F= fréquence en Hz
Différents types de moteurs ?
Et bien essayons d’analyser les constituions interne du moteur asynchrone monophasé
Il existe sur le marché différents types de moteurs à phase auxiliaire, conçus pour répondre à des besoins spécifiques. Vous en étudierez deux modèles :
– le moteur à phase résistive ;
– le moteur à capacité au démarrage.
Moteur à phase résistive
– L’enroulement de marche de ce type de moteur possède un grand nombre de spires de gros fil, entraînant une grande réactance inductive (L) et une petite résistance (r).
– L’enroulement de démarrage se compose d’un plus petit nombre de spires réalisées avec un fil de plus petite section, provoquant une réactance inductive plus faible (l) et une résistance plus grande (R) que celles de l’enroulement de marche.
La figure suivante présente le diagramme vectoriel de ce type de circuit. Remarquez le déphasage des courants Imarche et Idémarrage par rapport à la tension E. Le courant qui en résulte est identifié par l’abréviation I.
Diagramme vectoriel d’un moteur monophasé à phase résistive :
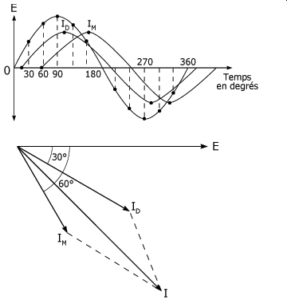
Puisque le courant de marche est déphasé par rapport au courant de démarrage, les champs magnétiques qui en résultent le sont aussi et favorisent ainsi le champ magnétique tournant nécessaire au démarrage du moteur.Lorsque le moteur atteint 75 % de sa vitesse nominale, l’interrupteur centrifuge débranche l’enroulement de démarrage. Le moteur se comporte alors comme un moteur asynchrone et tourne à une vitesse légèrement inférieure à sa vitesse synchrone. Nota : A cause du temps de réaction relativement élevé de l’interrupteur (jusqu’à deux secondes), le moteur à phase résistive se prête mal à des démarrages fréquents. Parmi ses applications, mentionnons le fonctionnement de diverses machines-outils. Il reste malgré tout peu utilisé.
Moteur à condensateur de démarrage
Beaucoup plus fréquent, le moteur condensateur de démarrage ressemble au moteur à phase résistive. Un condensateur est toutefois relié en série avec l’enroulement de démarrage, ce qui permet d’accroître le déphasage entre les champs magnétiques. La puissance des moteurs à condensateur de démarrage s’échelonne de 1/20 à 10 kW.Le diagramme vectoriel de ce type de circuit apparaît à la figure suivante.Comme vous pouvez le constater, le déphasage entre le courant de marche et le courant de démarrage est plus grand que dans le cas d’un moteur à phase résistive. Cela permet d’obtenir un plus grand couple de démarrage.Diagramme vectoriel d’un moteur à condensateur de démarrage :
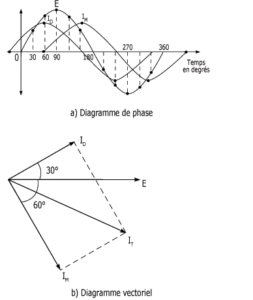
Lorsque la vitesse du moteur atteint 75 % de sa vitesse nominale, l’enroulement de démarrage et le condensateur sont débranchés du circuit.
Cette action est réalisée par un interrupteur centrifuge ou un contact temporisé. Le moteur se comporte alors comme un moteur à phase résistive.
Puissance pour un moteur
Lorsqu’une installation appelle 10 ampères au réseau, il ne faudra considérer dans ce courant que la composante qui est en phase avec la tension, qui agit en synchronisme avec le réseau : on parle de composante active ou de courant actif. C’est ce courant qui va développer de la puissance, encore appelée puissance “active”. P=U*I*cos (phi)
U est la tension efficace (en volts), I le courant efficace (en ampères). phi est le déphasage entre la tension et le courant : si l’utilisateur emploie plein de moteurs avec de la self, phi peut s’écarter notamment de zéro (zéro correspond à l’origine des phases pour une tension U on commence à 0).
Problème : le consommateur paie U*I*cos(phi) tandis que EDF doit dimensionner ses installations pour produire un courant I. EDF parle donc de puissance apparente U*I, il en va de même pour un fabricant de groupes électrogènes qui spécifie ses engins en volts.ampères (souvent en kilo volts ampères kVA). D’ailleurs les pertes en ligne dépendent de I² et pas de cos(phi).
En conséquence, EDF va exiger que le consommateur ajuste son installation avec des condensateurs ou autres pour ramener cos(phi) à une valeur par exemple supérieure à 0,8, sinon il est pénalisé.
La puissance réactive U*I*sin(phi) est l’autre “composante” de la puissance.
On peut dire qu’un condensateur consomme de la puissance réactive, ce qui revient à dire que phi diminue.
La puissance réactive c’est quoi ?
Beaucoup de personne se pose cette question et peut-être vous alors ? si vous lisez ce paragraphe. La puissance active, serait la composante de la puissance apparente, qui, venant en amont du circuit, l’alimenter. La puissance active sert par exemple à mettre en mouvement un moteur, effectuer une “action physique” “perceptible. En ce qui concerne la puissance réactive, celle-ci qui est engendré par bobine ou condo se n’est pas une puissance qui sert à faire “tourner les machine”. EDF facture et demande de la minimiser (a l’aide de condensateur) car plus elle est grande plus I est grand.
En définitive, il y’a 3 types de puissance mais nous ne pouvons pas transformer la puissance réactive (qui sert a rien pour schématiser) pour quelle devienne active elle est réellement absorbé par le moteur ou autre.
La puissance réactive n’a de puissance… que le nom !
En fait, la seule puissance au sens mécanique du terme (l’expression d’un travail réalisé dans un temps donné), c’est la puissance active qui la fournit.
La puissance réactive Q est définie par analogie à la puissance active P : Q=U*I*sin (phi)
Elle s’exprime en VAr ou VAR, abréviation de “volt-ampère-réactif”.
Son intérêt provient du fait qu’elle permet d’évaluer l’importance des récepteurs inductifs (moteurs, lampes fluorescentes, ….) et des récepteurs capacitifs (condensateurs, …) dans l’installation.
Les compteurs récemment installés vont d’ailleurs enregistrer distinctement la puissance réactive inductive et la puissance réactive capacitive.
Conclusions
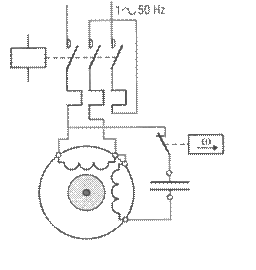
A la mise sous tension un courant parcourt les bobines du stator entrainant un flux magnétique à la fréquence de 50Hz. Puisque le bobinage étant monophasé, le flux étant des deux coté opposé, les forces mécaniques s’annulent Il est donc impératif de mettre en place un condensateur de démarrage, qui améliore le couple et sert aussi à lancer le moteur. Il est tout à fait possible de mettre des condensateurs, plus important pour augmenter d’avantage le couple, mais ce qu’il faut ce dire c’est que le bobinage est de fil très fin et risquerais de «bruler », je vous déconseille de mettre des valeurs de condensateur supérieur à ce que préconisent le(s) constructeur(s).
Quoi de plus facile que de brancher un moteur monophasé
2 fils et la terre. Hélas le problème devient plus hardi lorsque l’on veut changer le sens de rotation car justement il n’y a que 2 fils !!!!
le type le plus fréquent dans la vie de tous les jours 95 % des moteurs vendus, mais 25 % de la consommation électrique généralement de basse puissance
- applications : • réfrigérateurs
- lave-vaisselle
- laveuses
- …
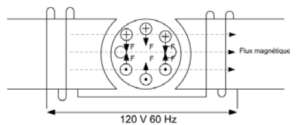
Tout comme le moteur triphasé, des courants sont induits dans cage d’écureuil, MAIS lorsque le moteur est à l’arrêt, le champ n’est pas tournant, à l’arrêt, le rotor est soumis à forces égales mais opposées.
et si on lance le rotor à la main ?
Flux dû au courant statorique & flux dû au courant rotorique donne naissance à un champ tournant
vitesse du champ = vitesse synchrone
phénomène complexe !
mise en rotation du rotor !
production d’un couple
vitesse se stabilise sous la vitesse synchrone
Comment démarrer le moteur ?
Il faut créer un champ tournant de démarrage, pour créer un champ tournant, il suffit de deux phases décalées spatialement de 90° et parcourues par des courants déphasés au plus le déphasage entre les courants est proche de 90°, au plus le champ aura une variation “circulaire ”et le couple produit par le rotor sera grand et constant.
Comment créer deux phases à partir du réseau monophasé ?
Rajouter un bobinage supplémentaire, dit bobinage de démarrage, en parallèle avec le bobinage principal, à 90° degrés du bobinage principal, dit bobinage de marche.
Comment créer un déphasage entre les courants de chaque bobinages ?
En donnant un diamètre différent aux deux bobinages (moteurs à phase auxiliaire résistive)u
En rajoutant une capacité en série avec le bobinage de démarrage (moteurs à phase auxiliaire capacitive)
Selon les lois de l’électricité, ces deux effets créent un déphasage de courant.
Inversion du sens de rotation en monophasé:
L’inversion de sens de rotation d’un moteur monophasé peut s’avérer de très facile à plus compliquée suivant le type de moteur mono.
Il faut en effet distinguer 2 catégories en mono tension 230 Volts :
Monophasé Biphasé
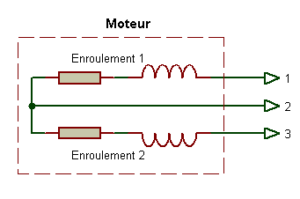
Bobinage monophasé:
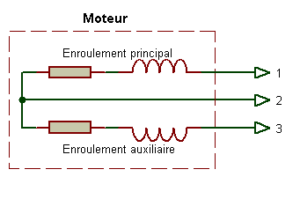
Le bobinage en monophasé avec 2 enroulements : 1 enroulement principal et 1 enroulement auxiliaire (la résistance de l’enroulement auxiliaire est supérieure à celle du principal car les enroulement sont fin et donc la résistance élevée).
(4 fils)

Bobinage en biphasé
Avec 2 enroulements distincts de mêmes caractéristiques.
Moteur 3 fils de sorties
Avec 3 fils de sorties monophasé et biphasé peuvent êtres confondus :
Pour repérer le monophasé du biphasé il n’y a qu’une solution c’est celle de mesurer à l’ohmmètre la résistance des enroulements entre 1, 2 et 3, tout en ayant connaissance que dans un «type monophasé » la résistance de l’enroulement auxiliaire est beaucoup plus grande que celle de l’enroulement principal, et dans le «type biphasé » les 2 enroulements sont identiques.
Dans le 1er cas (monophasé) les mesures entre :
– 1 et 3, la résistance va être supérieure
– 1 et 2, la résistance va être inférieure
– 3 et 2 la résistance va être moyenne
Dans le 2ème cas (biphasé) les mesures entre :
– 1 et 3, la résistance va être supérieure
– 1 et 2 ou 3 et 2, la résistance va être inférieure à 1 et 3 mais égale entre 1et 2 ou 3 et 2.
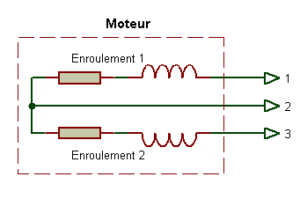
C’est uniquement par comparaison et en connaissant le type de mesure que l’on peut déterminer quel est le type de couplage du moteur.
Donc pour 3 fils de sorties : dans le cas du moteur biphasé aucun problème pour l’inversion, pour le cas du monophasé il n’y a pas d’autre solution que de reprendre les connexions au stator.
Inversion monophasé
Le principe d’inversion du sens de rotation est toujours le même : les 2 enroulements étant branchés en parallèles, il suffit d’inverser un enroulement par rapport à l’autre
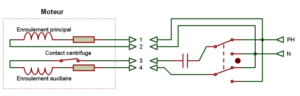
à noter que le moteur peut posséder un contact centrifuge il est incorporé au moteur, dans le cas contraire il faudra rajouter un relais d’intensité ou relais électronique
Inversion biphasé
Il suffit d’intervertir l’alimentation secteur aux bornes du condensateur pour le changement de rotation du moteur.
Artifice de démarrage: “Condensateur permanent ou de démarrage?”
Voir aussi:
Moteur monophasé (condensateur de démarrage)
Moteur monophasé (condensateur permanent)
Pour pouvoir fournir une intensité plus importante à l’enroulement de démarrage, nous devrons utiliser un condensateur.
Rôle du condensateur :
le condensateur va permettre de donner un surplus d’intensité de sorte à obtenir le déphasage nécessaire a la phase auxiliaire.
Il existe 2 sortes de condensateur de démarrage :
Les condensateurs de marche (dis de permanence): qui ont une faible capacité (rarement plus de 30 microfarads uF) sont conçus pour rester sous tension en permanence sans aucun échauffement excessif.
Les condensateurs de démarrage: possèdent une importante capacité pouvant dépasser les 100 microfarads. Ils doivent absolument pas resté sous tension sinon ils s’échauffent très rapidement et risquent d’exploser. (un contact centrifuge va venir s’ouvrir et ainsi déconnecter le condensateur de démarrage)
Choix d’un moteur monophasé
à phase auxiliaire résistive :
- Le plus courant, pour couples de démarrage moyens.
- Démarrages peu fréquents.
- 60 W- 250 W.
- Pour ventilateurs, pompes centrifuges, machines à laver, brûleurs, petites machines-outils telles que des tours, des meules, etc.
à phase auxiliaire capacitive :
Voir aussi => Moteur monophasé (condensateur de démarrage)
- Pour forts couples de démarrage ou charges de grandes inerties.
- 0.5 kW – 8 kW.
- Pour outils fixes tels scies de table, compresseurs; appareils domestiques (aveuses, séchoir à linge, équipement de ferme, convoyeurs); gros ventilateurs, des pompes à piston, etc.
à condensateurs permanents : Voir aussi => Moteur monophasé (condensateur permanent)
- Pour faible couples de démarrage.
- Faible puissance car mauvais rendement.
- Simples; robustes, faibles coûts de maintenance.
- Silencieux.
- Pour les séchoirs à cheveux, humidificateur, four à micro-ondes, etc.
universels série :
- Pour grandes vitesses.
- Pour poids et encombrement faibles.
- Pour outils portatifs, aspirateurs domestiques, petites machines-outils.
Etude du moteur asynchrone
Document technique à télécharger Calculs du couple electromagnetique
La machine asynchrone est, de par sa construction, la machine la plus robuste. C’est elle qui est utilisée dans les machines à laver, les ventilateurs de garage ou entrepôts, etc. À la suite des trains à grande vitesse allemands, les TGV français sont maintenant motorisés à l’aide de ce type de moteur. La machine asynchrone est rarement utilisée pour les conversions de très forte puissance (supérieure à 100 MW) et sa réversibilité nécessite de l’électronique de puissance.
Bilan de puissance modèle équivalent

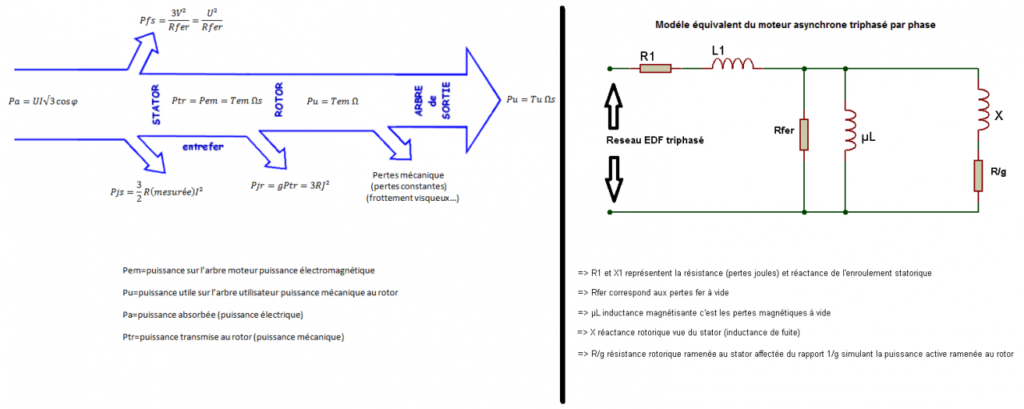
Pour trouver les valeurs des éléments, on effectue 3 essais :
– un essai en continu pour mesurer la résistance statorique par phase (R1).
– un essai à rotor bloqué pour déterminer la résistance du rotor (R/g) et la réactance de fuite au rotor X.
– un essai à vide (ou mieux encore, à vitesse de synchronisme) pour obtenir les pertes dans le fer (dans Rfer) et l’inductance magnétisante (µL).
1er essais mesures
Lorsque le moteur asynchrone triphasé équilibré est couplé en étoile, à l’aide d’un ohmmètre on peut mesurer la résistance du stator, ou en utilisant un montage voltampèremétrique, sous une tension continu, on peut aussi mesurer la tension et le courant (sans dépasser In). On obtient à l’aide de ce dernier montage la valeur de la résistance en appliquant la loi d’ohm : R1 = U / 2I.
Couplage ETOILE
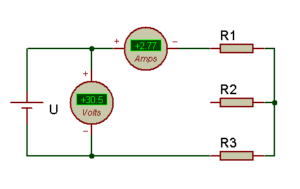
Couplage TRIANGLE
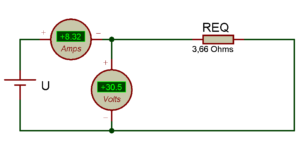
Afin de déterminer la résistance aux bornes d’un enroulement mais cette fois-ci en couplage triangle, il faut déterminer la résistance équivalente du montage qui est égale à REQ=U/I. Avec une tension mesurée de U=30,5V et un courant mesuré de I=8,32A la résistance équivalente est REQ=U/I=30,5/8,32=3,66 Ohms
On peut donc représenter le montage triangle de cette façon :
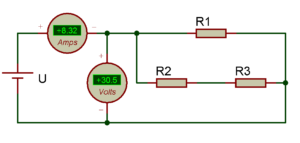
Nous avons R1 en parallèle avec R2 et R3. Mais ! il faut savoir que pour un moteur asynchrone triphasé les 3 enroulements sont censés être équilibrés ! Nous avons donc R1=R2=R3=R soit :
R en parallèle sur 2R donne par calcul :
REQ = (R*2R) / (R + 2R) = 2R²/3R = 2/3*R
REQ = 2/3 * R
On peut aussi calculer de la même façon avec :
1/REQ = 1/R + 1/2R = (2R+R) /2R² = 3R/2R² = 3/(2R)
REQ = 2/3*R
Bon !! Revenons à nos moutons !!Si REQ = 3,66 Ohms, alors la résistance d’un seul enroulement est égale à R = (3/2)*REQ = (3/2) * 3,66 = 5,49Ohms soit 5,5 Ohms identique au précédent.
2ème essais à vide
à savoir:
le moteur asynchrone est équivalent à un transformateur dont l’enroulement secondaire (rotor), est en rotation
C’est un essai à vide. Si on considère que la vitesse à vide est très proche de la vitesse nominale, on a un glissement gvide = 0 . Dans ce cas, la résistance R/g est infinie et le schéma équivalent par phase du moteur devient proche de :
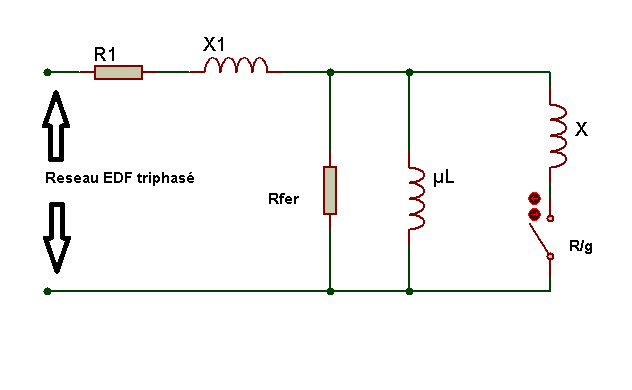
MODELE EQUIVALENT PAR PHASE lors de l’essai à vide (hypothèse g=0)
Pour faciliter le calcul on négligera la réactance X1, ainsi le nouveau schéma équivalent donne:
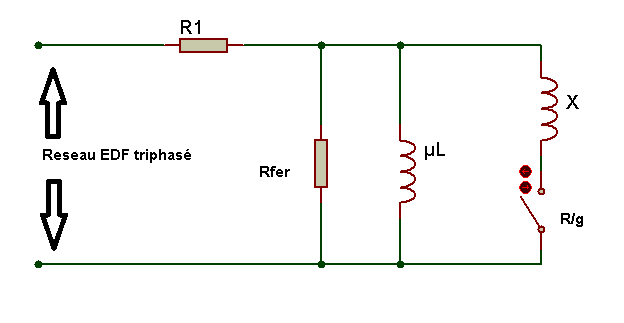
La mesure des puissances active et réactive permet donc de calculer Rfer et Xm . Les résultats des mesures sont les suivantes :
Pv = 186 W
Qv = 1.14 Kvar
U = 400 V (tension sur 1 enroulement : V = 230 V)
Iv = 1.66 A (montage étoile)
CALCULS
Les pertes joules statoriques sont de :
Pjs=3R1Iv²=3*5,5*1,66²=45,46W.
Si on considère que le glissement est nul, les pertes dans le fer sont donc telles que :
Pfer=Pv-Pjs=186-142=140,54W.
On peut en déduire Rfer :
Rfer=3V²/Pfer=(3*230²)/140,54=1129ohms.
De même, pour la réactance magnétisante, on obtient :
µL= 3V²/Qv=(3*230²)/1140=139ohms
3ème essais en court-circuit
Il consiste à effectuer des mesures à rotor bloqué (sous tension réduite et courant nominal). Dans ce cas, le glissement est égal à un. Les puissances dans Rfer et dans µL deviennent négligeables devant les autres (elles sont proportionnelles au carré de la tension d’alimentation).
Cet essai nous permet de calculer R/g et X.
La manipulation se réalise de la façon suivante : on met la commande du frein à 100% (ne pas oublier de mettre en route la ventilation du frein, et effectuer la mesure assez rapidement), puis on augmente très progressivement la tension jusqu’à avoir le courant nominal (In =Icc= 3.2 A), enfin on mesure les puissances active et réactive.
Les résultats de ces essais sont les suivants :
Pour 1 phase : Pcc = 87 W
Qcc = 123 var
Ucc = 82 V (tension aux bornes d’un enroulement : 47.3 V)
Icc = 3.18 A (montage étoile)
CALCULSOn calcule, par phase, la puissance dissipée dans R, lors de l’essai à rotor bloqué :
P=Pcc-R1*Icc²=87-(5,5*3,18²)=31,38W.
On en déduit les valeurs de R et X (toujours en négligeant les puissances dans Rfer et µL)
R=Pcc/Icc²=31,38/3,18²=3,1 ohms et X=Qcc/Icc²=123/3,18²=12,16 ohms
Remarque :
En réalité, on devrait recalculer la tension V’ aux bornes de Rfer et µL
Pfer=Pv-Pjs=140,54W
S’=(racine (Pfer²+Qv²)/3)=(racine(140,54²+1140²)/3)=382Var
V’=S’/I=382/1,66=230V .
On a donc bien fait de négliger la chute de tension aux bornes de R1.
En réalité, lors de la mesure à vide, on n’est pas tout à fait à la vitesse de synchronisme. Si on veut faire réellement la mesure au synchronisme, on doit amener le moteur asynchrone à cette vitesse en l’entraînant, par exemple, par le moteur à courant continu.
Résumé:
R1 = 5,5 Ω
µL = 139 Ω
R= 3,1 Ω
X = 12,2 Ω => L=X/(2.pi.f)=12,2/(2*3,14*50)=0,0388 H
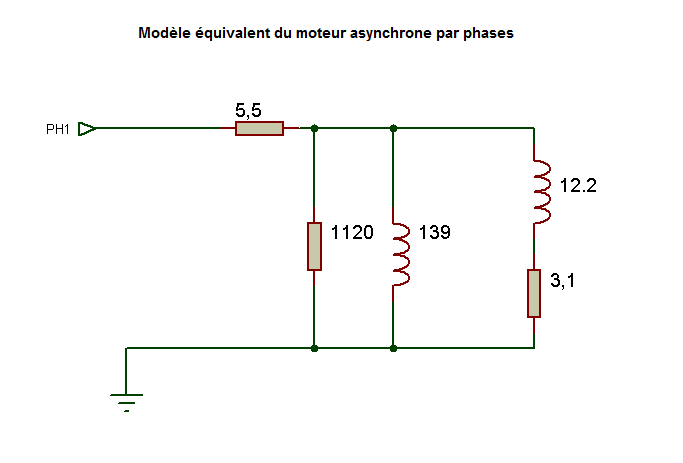
Vous trouverez la Note de calcul
Triphasé équilibré
Couplage étoile (Y), pour un moteur, plus petite tension admissible aux bornes d’un enroulement.
le courant en ligne
I=J => I1=I2=I3=0 (vectoriel)
Puissance en W (watt) =>puissance active ou wattée
P=U.I.√3.cos Fi I courant en ligne
Puissance en Var => puissance réactive (volt ampère réactif)
Q=U.I.√3.sin Fi I courant en ligne
Puissance en VA=> puissance apparente (volt ampère)
S=U.I.√3=√(P²+Q²) I courant en ligne
Cos Fi=P/S => sin Fi=Q/S
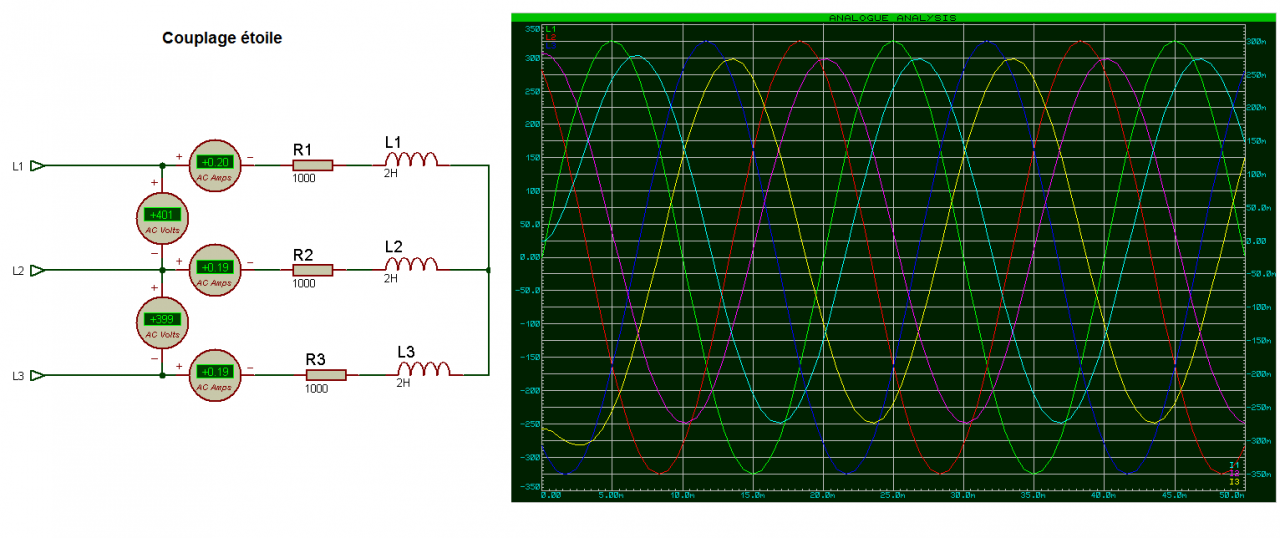
Calculs :
Impedance charge: Z=√(R²+(Lw)²)=(1000²+(2*2*pi*50)²)=1181 ohms
I=V/Z=230/1181 (couplage étoile)=0,19A
Cos Fi=R/Z= (1000/1181)=0,84 => sin Fi=Lw/Z=0,53
P=U.I.√3.cos Fi=400*0,19*√3*0,84=110W
Q=U.I.√3.sin Fi=400*0,19*√3*0,54=71Var
S=U.I.√3=400*0,19*V3=131VA
Cos Fi=(P/S)=110/131=0,84 => sin Fi=(Q/S)=0,54
Le courant est déphasé de 32,90 par rapport à la tension, la tension est en avance sur le courant donc le courant est en retard.
L1 en avance de 32,9° sur I1
L2 en avance de 32,9° sur I2
L3 en avance de 32,9° sur I3
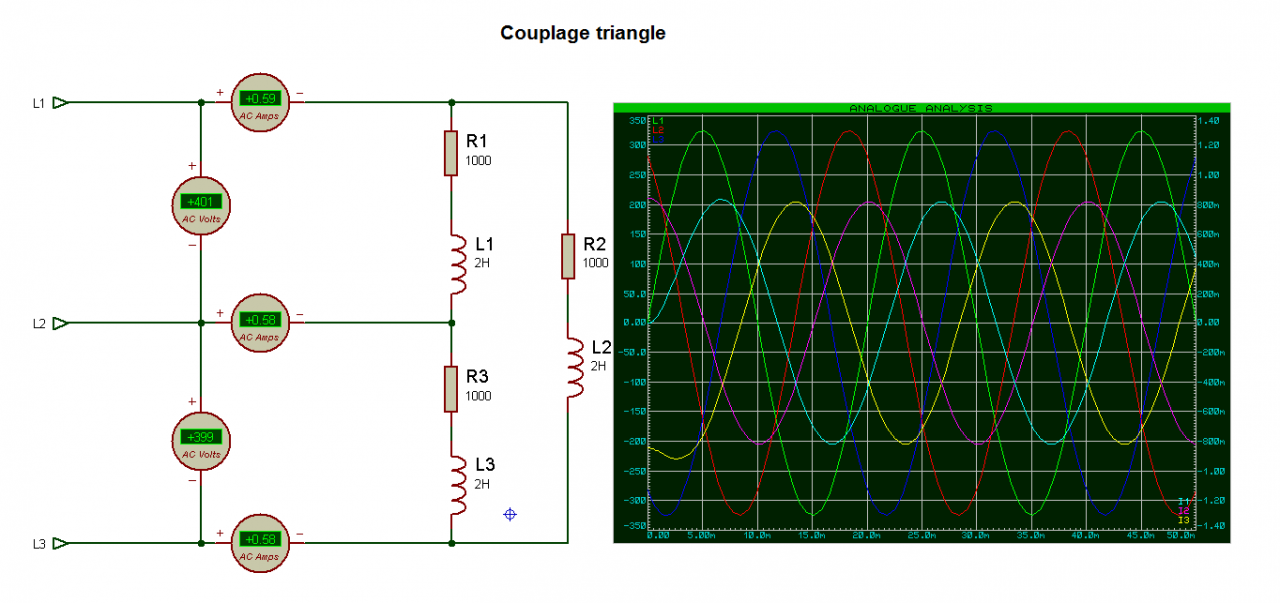
Couplage triangle (Δ), pour un moteur triphasé, plus grande tension admissible aux bornes de 2 enroulements
le courant en ligne I=J√3 I1=I2=I3=0 (vectoriel) =>
Equilibré ou déséquilibré la sommes des courants toujours égales à zéro.
(Voir aussi=> Montage triphasé (déséquilibré))
I1=J12-J31 (vecteurs)
I2=J23-J12 (vecteurs)
I3=J31-J23 (vecteurs)
Puissance en W (watt)=>puissance active ou watté
P=U.I.√3.cos Fi I courant en ligne
Puissance en Var=> puissance réactive (volt ampère réactif)
Q=U.I.√3.sin Fi I courant en ligne
Puissance en VA=> puissance apparente (volt ampère)
S=U.I.√3=√(P²+Q²) I courant en ligne
Cos Fi=P/S => sin Fi=Q/S
Calculs :
Impedance charge: Z=√(R²+(Lw)²)=(1000²+(2*2*pi*50)²)=1181 ohms
J=U/Z=400/1181 (couplage étoile)=0,33A
I=J.√3=0,33*√3=0,59A
Cos Fi=R/Z= (1000/1181)=0,84 => sin Fi=Lw/Z=0,53
P=U.I.√3.cos Fi=400*0,59*√3*0,84=343W
Q=U.I.√3.sin Fi=400*0,59*√3*0,54=220Var
S=U.I.√3=400*0,59*V3=408VA
Cos Fi=(P/S)=110/131=0,84 => sin Fi=(Q/S)=0,54
Le courant est déphasé de 32,60 par rapport à la tension, la tension est en avance sur le courant donc le courant est en retard.
L1 en avance de 32,6° sur I1 (inchangé)
L2 en avance de 32,6° sur I2 (inchangé)
L3 en avance de 32,6° sur I3 (inchangé)
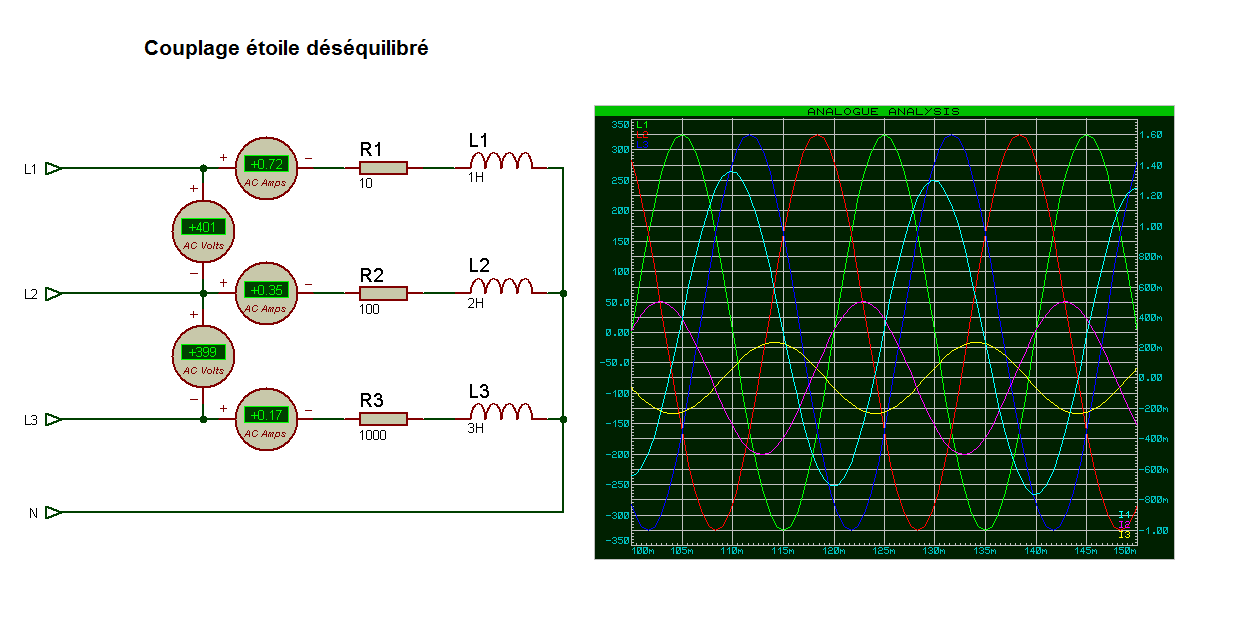
Montage triphasé déséquilibré
Couplage étoile (Y), pour un moteur, plus petite tension admissible aux bornes d’un enroulement.
le courant en ligne I=J => I1=I2=I3≠0 (vectoriel) => Neutre obligatoire triphasé déséquilibré
Puissance en W (watt) =>puissance active ou wattée
P=U.I.√3.cos Fi I courant en ligne => NE FONCTIONNE PLUS EN DESQUILIBRE
Puissance en Var => puissance réactive (volt ampère réactif)
Q=U.I.√3.sin Fi I courant en ligne => NE FONCTIONNE PLUS EN DESQUILIBRE
Puissance en VA=> puissance apparente (volt ampère)
S=U.I.√3=√(P²+Q²) I courant en ligne => NE FONCTIONNE PLUS EN DESQUILIBRE
Cos Fi=P/S => sin Fi=Q/S
Calculs :
Lorsque le montage est déséquilibré, il faut calculer dans chaque « branches » le courant I.
Branche 1 :
Impedance charge: Z1=√(R1²+(L1w)²)=(10²+(1*2*pi*50)²)=314 ohms
I1=V1/Z1=230/314 (couplage étoile)=0,732A
Cos Fi1=R1/Z1= (10/314)=0,032 => sin Fi1=L1w/Z1=1
P1=V1.I1.cos Fi1=230*0,732*0,032=5,38W
Q1=V1.I1.sin Fi1=230*0,732*0,99=168,25Var
S1=V1.I1=230*0,732=168,25VA
Cos Fi1=(P1/S1)=5/168,25=0,032 => sin Fi1=(Q1/S1)=0,999
Le courant I1 dans la branche 1 est déphasé de 88° par rapport à la tension, la tension est en avance sur le courant donc le courant est en retard d’environ 90° (purement inductif)
Branche 2 :
Impedance charge: Z2=√(R2²+(L2w)²)=(100²+(2*2*pi*50)²)=636 ohms
I2=V3/Z2=230/636 (couplage étoile)=0,362A
Cos Fi2=R2/Z2= (100/636)=0,157 => sin Fi2=L2w/Z2=0,98
P2=V2.I2.cos Fi2=230*0,362*0,157=13,07W
Q2=V2.I2.sin Fi2=230*0,362*0,98=81,59Var
S2=V2.I2=230*0,362=83,26VA
Cos Fi2=(P2/S2)=12,45/82,8=0,157 => sin Fi2=(Q2/S2)=0,98
Le courant I2 dans la branche 2 est déphasé de 81° par rapport à la tension, la tension est en avance sur le courant donc le courant est en retard.
Branche 3 :
Impedance charge: Z3=√(R3²+(L3w)²)=(1000²+(3*2*pi*50)²)=1374 ohms
I3=V3/Z3=230/1374 (couplage étoile)=0,167A
Cos Fi3=R2/Z2= (1000/1374)=0,727 => sin Fi3=Lw/Z=0,685
P3=V3.I3.cos Fi3=230*0,167*0,727=27,92W
Q3=V3.I3.sin Fi3=230*0,167*0,685=26,345Var
S3=V3.I3=230*0,167=38,41VA
Cos Fi3=(P2/S2)=26,49/36,8=0,727 => sin Fi3=(Q2/S2)=0,685
Le courant I3 dans la branche 3 est déphasé de 43° par rapport à la tension, la tension est en avance sur le courant donc le courant est en retard.
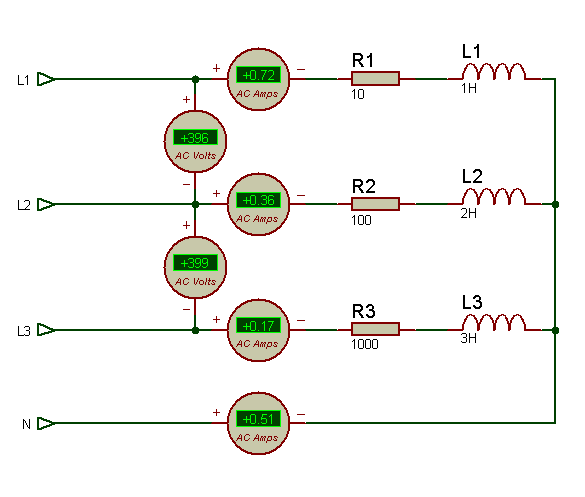
La puissance totale consommée aux bornes du montage est la somme de :
P1+P2+P3=Pt (vectoriel)
Q1+Q2+Q3=Qt (vectoriel)
St=√(Pt²+Qt²)
P1+P2+P3=5,38+13,07+27,92=46,37W
Q1+Q2+Q3=167,9+74,52+25,39=276,185Var
St=√(Pt²+Qt²)=√(46,37²+267,185²)=280Va
I=In=S/V=280/230=1,21A
Ou autre méthode :
Pour trouver le courant dans le neutre, il suffit d’ additionner I1+I2+I3=In (vectoriellement), le courant dans le neutre existe ne SURTOUT JAMAIS COUPER OU RETIRER LE NEUTRE !!!
En passant par les nombres complexes :
I1=[0,732 ; 88°]=0,73*cos 88+0,73*sin 88=0,025+j 0,729
I2=[0,362 ; 81°]=0,36*cos 81+0,36*sin 81=0,056+j 0,355
I3=[0,167 ; 43°]=0,16*cos 43+0,16*sin 43=0,117+j 0,109
In=I1+I2+I3=0,025+j 0,73+0,05+j 0,35+0,11+j 0,110=0,204+j 1,193
In=[1,210 ; 80°]
le tableau ci-dessous donnes des valeurs précises car tous les chiffres après la virgule sont pris en compte.
![]()
La sécurité des machines
Ci-dessous un lien permettant de télécharger des documents techniques
– La sécurité des machines
Ci-dessous un lien permettant de télécharger des documents techniques
– Installations tertiaires
Inerties (calculs)
Lorsque dans un système d’entraînement, des masses tournent à des vitesses différentes, ou se déplacent en mouvement linëaire, il faut ramener leur moment d’inertie à la fréquence de rotation du moteur.
Le moment d’inertie pour une charge tournante à la vitesse (Ns) ou (ws), ramené à la vitesse du moteur (Ne) ou (we):
Js : Inertie en sortie
Je : inertie en entrée
Ws : vitesse angulaire en sortie
We : vitesse angulaire en entrée
Ns : vitesse en tr/min en sortie
Ne : vitesse en tr/min en entrée
Js=Je(Ne/Ns)²=Je(we/ws)²
Le moment d’inerttie d’une masse M en mouvement à la vitesse V ramenée à la vitesse w du moteur
J=M(v/w)²
Dernière mise à jour le 23/09/2013
Présentation
Ce montage électronique permet de faire de la variation d’intensité lumineuse. La structure de l’ensemble est composé de composants passifs.
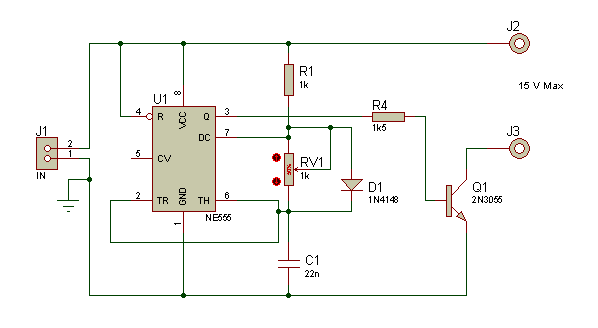
Schéma
Fonctionnement
Le circuit fait appel à un classique NE555 pour générer un signal périodique rectangulaire de fréquence “relativement” fixe, mais la largeur d’impulsions peut varier grâce au potentiomètre RV1.
L’oscillateur
L’oscillateur est bâtît sur un NE555 avec ses classiques composants satellites RV1, R2 et C1, dont les valeurs déterminent la fréquence d’oscillation et le rapport cyclique.
Interface de sortie
La sortie du NE555 (borne 3) n’est pas en mesure de délivrer un courant suffisant pour piloter directement une ampoule ou un moteur, aussi ce circuit intégré est-il épaulé par un transistor de puissance de type 2N3055, qui fait ainsi office d’interface de puissance. Le choix du transistor s’est porté sur un 2N3055 car ce dernier supporte bien des pointes de courant de plusieurs ampères. Sachez en effet qu’une ampoule électrique à filament, lorsqu’elle est éteinte, présente une résistance “à froid” dix à quinze fois inférieure à sa résistance “à chaud” (quand elle est allumée). Ainsi, une ampoule de 12W, qui consomme environ 1A en régime allumée, provoque une pointe de l’ordre de 10A lors de son allumage (ce à quoi l’alimentation pourra certainement répondre pendant un court instant).
En ce qui concerne le transistor 2N3055, celui-ci à un gain pour une température de 25°C et pour un courant de 8A (courant Ic) de G=20. Avec un gain de 20et un courant de collecteur de 8A on ce retrouve avec un courant de 0,4A !!!! dans ce cas notre petit circuit intégré NE555 va nous débiter un courant de 0,4A ?? (non je ne pense pas).
En regardant le Datasheets de ce dernier, celui-ci à des valeurs max à ne pas dépasse d’ailleur tension max = 18 V, nous sommes donc pile à la limite, ce qui est forcément risqué…
En ce qui concerne le courant de sortie de notre NE555 (Icc=10mA pour une tension de 15V maxi 15mA, mais je préfère rester en dessous.)
Prenons un courant de sortie de 10mA le transistor va donc avoir dans sa base un courant de 10mA qui va le parcourir, pour un courant de 10mA le courant Ic est proche de 1A, pour un courant de 12mA la chute de tension Vce est de l’ordre de 1,6V et la chute de tension Vbe=0,8V.
La résistance qui va venir limité le courant évitant la destruction de notre NE555 est de 1k4 normalisé 1k5 (15-0,8)/0.010=R2.
Bon il est vrai que pour un tel courant de base le transistor ne va pas amplifier grand-chose seulement un gain de 75 (valeur indiqué sur la courbe du datasheet).
Regardons en ce qui concerne la simulation, je place un générateur de 15V, et qui débite un courant de 1A, avec une chute de tension de 1,6V aux bornes du transistor 2N3055, et je met une résistance de 1k5 pour avoir un courant de 10mA.
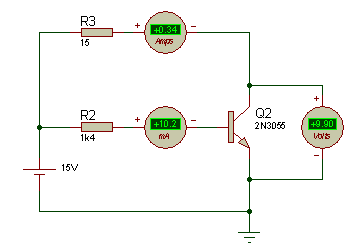
Tiens étonnant !! Aucune valeurs ne ressembles à mes calculs mise à part le courant Ib mais Vce et Ic??? Dequoi s’agit t’il ? est-ce une erreur de calcul (pourtant non), est-ce une erreur de lecture du datasheet (non) alors c’est quoi ?
Ahhh mais oui !!!, voila l’erreur la fonction de transfert de notre 2N3055 par rapport à la simulation. J’ai fais une analyse de mon transistor 2N3055 grâce à l’outils interne à proteus. Quand on regarde le courant de base, et le courant collecteur en aucun cas ces résultats sont identiques avec le datasheet du 2N3055.
Regardons ensemble le courant Ic pour 1A, et le courant Ib :
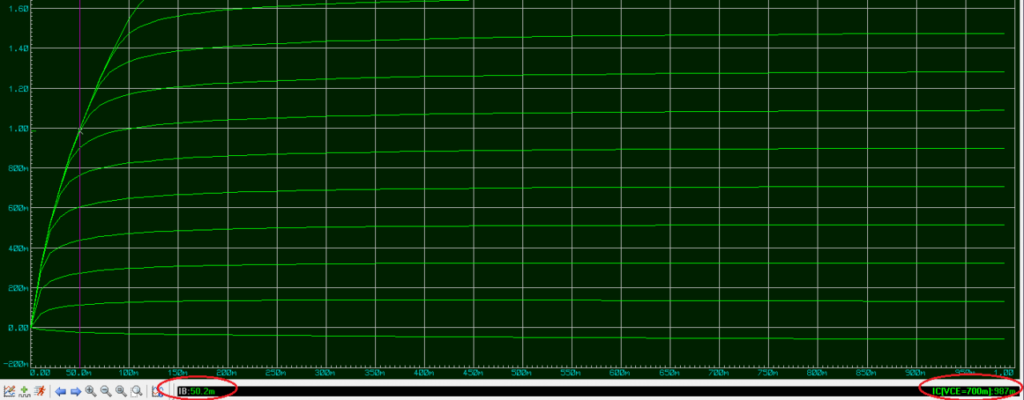
Pour un courant proche de 1A nous avons un Ib=50mA (environ) (différent de 10mA), alors la résistance R2 à donc une valeur de 284 Ohms (théorique) (15-0,8)/0.050=R2
Et pour un courant Ic=1A nous avons une chute de tension de 0,7V (différent de 1,6V)
Ic=(15-0,7)/1=14,3 Ohms (théorique) nous laisserons 15Ohms nous allons pas « chipoter » pour 0,7 Ohms…
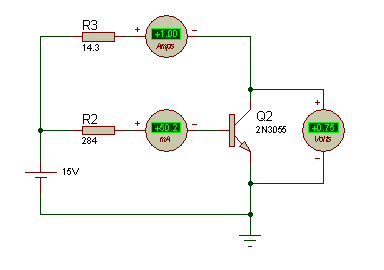
Alors ça par exemple !!!!
Mais une question alors, on se base sur quoi ? valeur théorique (logiciel) ou valeur pratique (datasheet), je vous laisses réfléchir…
(voir Théories fonction de transfert transistor NPN) pour les curieux…
Circuit imprimé
Historiques
23/09/2013
– 1er mise à disposition
Fonctionnement
Pour ceux qui ont lu ma page de calculs, il est évident que le potentiomètre RV1 a un rôle important dans ce montage filtre passe bas.
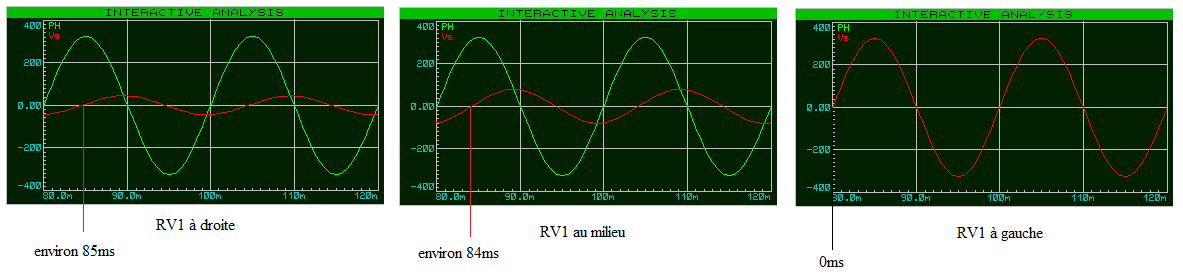
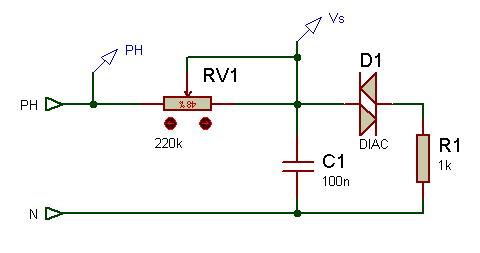
Ce qui est intéressant dans ce montage c’est que nos pouvons « jouer » sur la charge du condensateur, (retard à l’amorçage si on alimente un thyristor), On peut aussi assembler ce genre de montage avec un diac, comme ci-dessous.
Potentiomètre RV1
Le principe est le suivant, lorsque le condensateur va se charger à travers RV1, le potentiel Vs (potentiel de sortie) sera retardé en fonction de l’angle, ainsi le zéro de la sinusoïde tension d’entrée Ve, et le zéro de la sinusoïde tension de sortie Vs est décalé. Le temps de charge du condensateur commencera à partir d’un certain temps, et en ce qui concerne le diac, qui deviens conducteur lorsque la tension dépasse un certain seuil (tension de retournement) va devenir passant entrainent la décharge brutal du condensateur C1.
Diac
Le diac est un composant qui est passant à une certaine tension (50V), et va venir amorcer le thyristor U1. En modifiant la valeur du potentiomètre RV1, nous modifions la temps de charge C1 ce qui va modifier l’amorçage de U1.