Etude du moteur asynchrone
Document technique à télécharger Calculs du couple electromagnetique
La machine asynchrone est, de par sa construction, la machine la plus robuste. C’est elle qui est utilisée dans les machines à laver, les ventilateurs de garage ou entrepôts, etc. À la suite des trains à grande vitesse allemands, les TGV français sont maintenant motorisés à l’aide de ce type de moteur. La machine asynchrone est rarement utilisée pour les conversions de très forte puissance (supérieure à 100 MW) et sa réversibilité nécessite de l’électronique de puissance.
Bilan de puissance modèle équivalent

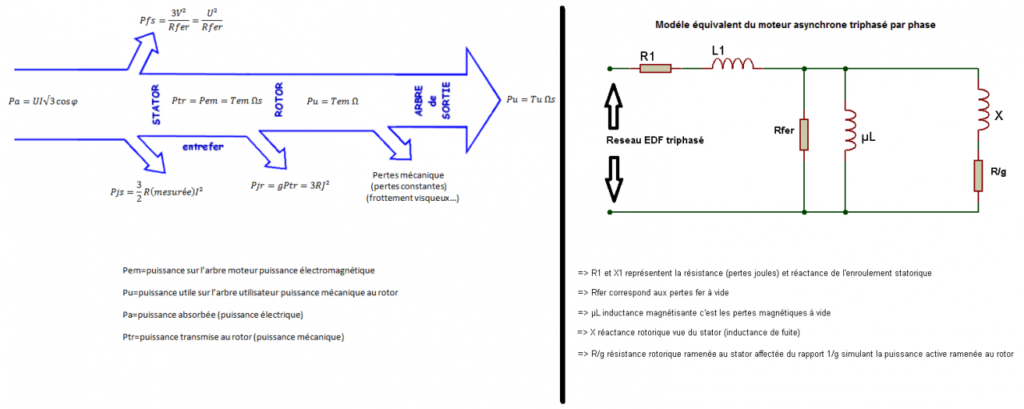
Pour trouver les valeurs des éléments, on effectue 3 essais :
– un essai en continu pour mesurer la résistance statorique par phase (R1).
– un essai à rotor bloqué pour déterminer la résistance du rotor (R/g) et la réactance de fuite au rotor X.
– un essai à vide (ou mieux encore, à vitesse de synchronisme) pour obtenir les pertes dans le fer (dans Rfer) et l’inductance magnétisante (µL).
1er essais mesures
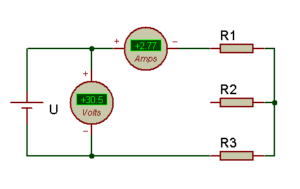
Lorsque le moteur asynchrone triphasé équilibré est couplé en étoile, à l’aide d’un ohmmètre on peut mesurer la résistance du stator, ou en utilisant un montage voltampèremétrique, sous une tension continu, on peut aussi mesurer la tension et le courant (sans dépasser In). On obtient à l’aide de ce dernier montage la valeur de la résistance en appliquant la loi d’ohm : R1 = U / 2I.
Couplage ETOILE
Couplage TRIANGLE
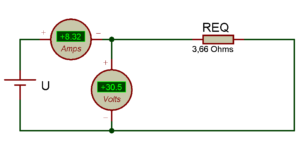
Afin de déterminer la résistance aux bornes d’un enroulement mais cette fois-ci en couplage triangle, il faut déterminer la résistance équivalente du montage qui est égale à REQ=U/I. Avec une tension mesurée de U=30,5V et un courant mesuré de I=8,32A la résistance équivalente est REQ=U/I=30,5/8,32=3,66 Ohms
On peut donc représenter le montage triangle de cette façon :
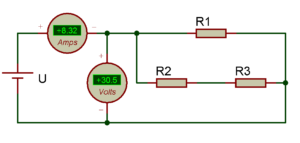
Nous avons R1 en parallèle avec R2 et R3. Mais ! il faut savoir que pour un moteur asynchrone triphasé les 3 enroulements sont censés être équilibrés ! Nous avons donc R1=R2=R3=R soit :
R en parallèle sur 2R donne par calcul :
REQ = (R*2R) / (R + 2R) = 2R²/3R = 2/3*R
REQ = 2/3 * R
On peut aussi calculer de la même façon avec :
1/REQ = 1/R + 1/2R = (2R+R) /2R² = 3R/2R² = 3/(2R)
REQ = 2/3*R
Bon !! Revenons à nos moutons !!Si REQ = 3,66 Ohms, alors la résistance d’un seul enroulement est égale à R = (3/2)*REQ = (3/2) * 3,66 = 5,49Ohms soit 5,5 Ohms identique au précédent.
2ème essais à vide
à savoir:
le moteur asynchrone est équivalent à un transformateur dont l’enroulement secondaire (rotor), est en rotation
C’est un essai à vide. Si on considère que la vitesse à vide est très proche de la vitesse nominale, on a un glissement gvide = 0 . Dans ce cas, la résistance R/g est infinie et le schéma équivalent par phase du moteur devient proche de :
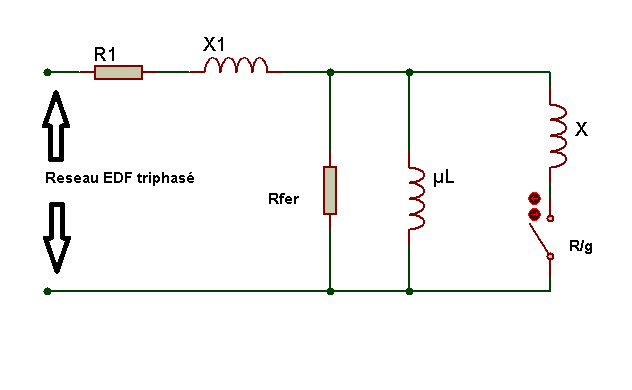
MODELE EQUIVALENT PAR PHASE lors de l’essai à vide (hypothèse g=0)
Pour faciliter le calcul on négligera la réactance X1, ainsi le nouveau schéma équivalent donne:
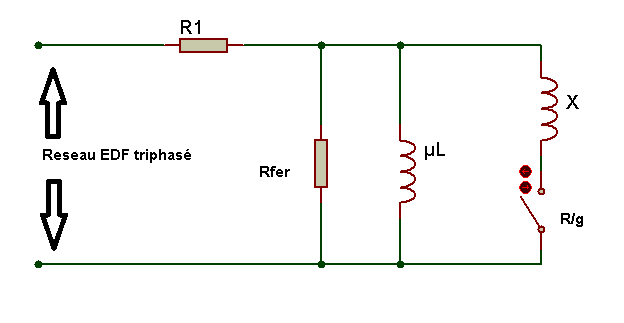
La mesure des puissances active et réactive permet donc de calculer Rfer et Xm . Les résultats des mesures sont les suivantes :
Pv = 186 W
Qv = 1.14 Kvar
U = 400 V (tension sur 1 enroulement : V = 230 V)
Iv = 1.66 A (montage étoile)
CALCULS
Les pertes joules statoriques sont de :
Pjs=3R1Iv²=3*5,5*1,66²=45,46W.
Si on considère que le glissement est nul, les pertes dans le fer sont donc telles que :
Pfer=Pv-Pjs=186-142=140,54W.
On peut en déduire Rfer :
Rfer=3V²/Pfer=(3*230²)/140,54=1129ohms.
De même, pour la réactance magnétisante, on obtient :
µL= 3V²/Qv=(3*230²)/1140=139ohms
3ème essais en court-circuit
Il consiste à effectuer des mesures à rotor bloqué (sous tension réduite et courant nominal). Dans ce cas, le glissement est égal à un. Les puissances dans Rfer et dans µL deviennent négligeables devant les autres (elles sont proportionnelles au carré de la tension d’alimentation).
Cet essai nous permet de calculer R/g et X.
La manipulation se réalise de la façon suivante : on met la commande du frein à 100% (ne pas oublier de mettre en route la ventilation du frein, et effectuer la mesure assez rapidement), puis on augmente très progressivement la tension jusqu’à avoir le courant nominal (In =Icc= 3.2 A), enfin on mesure les puissances active et réactive.
Les résultats de ces essais sont les suivants :
Pour 1 phase : Pcc = 87 W
Qcc = 123 var
Ucc = 82 V (tension aux bornes d’un enroulement : 47.3 V)
Icc = 3.18 A (montage étoile)
CALCULSOn calcule, par phase, la puissance dissipée dans R, lors de l’essai à rotor bloqué :
P=Pcc-R1*Icc²=87-(5,5*3,18²)=31,38W.
On en déduit les valeurs de R et X (toujours en négligeant les puissances dans Rfer et µL)
R=Pcc/Icc²=31,38/3,18²=3,1 ohms et X=Qcc/Icc²=123/3,18²=12,16 ohms
Remarque :
En réalité, on devrait recalculer la tension V’ aux bornes de Rfer et µL
Pfer=Pv-Pjs=140,54W
S’=(racine (Pfer²+Qv²)/3)=(racine(140,54²+1140²)/3)=382Var
V’=S’/I=382/1,66=230V .
On a donc bien fait de négliger la chute de tension aux bornes de R1.
En réalité, lors de la mesure à vide, on n’est pas tout à fait à la vitesse de synchronisme. Si on veut faire réellement la mesure au synchronisme, on doit amener le moteur asynchrone à cette vitesse en l’entraînant, par exemple, par le moteur à courant continu.
Résumé:
R1 = 5,5 Ω
µL = 139 Ω
R= 3,1 Ω
X = 12,2 Ω => L=X/(2.pi.f)=12,2/(2*3,14*50)=0,0388 H
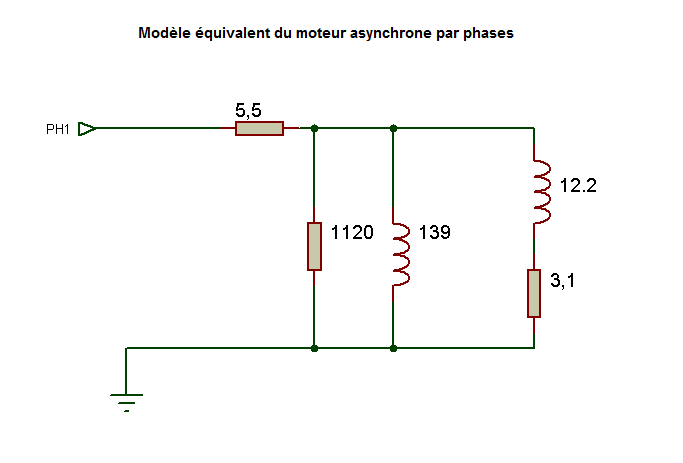
Vous trouverez la Note de calcul