Dernière mise à jour le 21/09/2013
Présentation
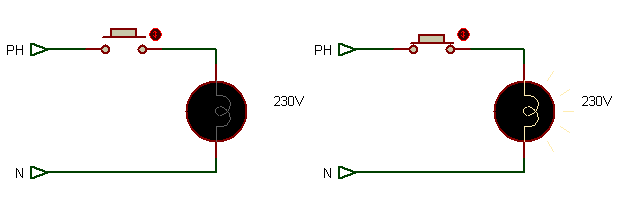
Si on mesure la résistance d’une ampoule à froid et qu’on la calcule ensuite à partir du courant qui parcourt le filament et de la tension à ses bornes, on constate une très grande variation. C’est que le tungstène qui constitue le filament est un métal dont la résistivité n’est pas constante.
Fonctionnement
La résistance à froid d’une ampoule à filament de tungstène d’une puissance de 60W a été mesurée égale à 60 ohms.
A chaud, c’est à dire soumise à une tension de 220 volts, on peut calculer avec la formule :
P = U² / R (avec P en W, U en volts et R en ohms)
que sa résistance s’établit à :
R = (220 x 220) / 60
R= 760 ohms.
En passant de 20 à 2700°C, le filament a vu sa résistance multipliée par 12.
Ce phénomène s’explique par le coefficient de température du tungstène.
En appliquant la formule
Rt°=R0[1+(a*dt°)], il est possible de déterminer la valeur de la résistance du filament.
Avec:
- R0 la résistance à froid
- a le coefficient de température du tungtène
- dt la différence de température entre froid et à chaud
En reprenant ce qui à été dis précédemment cela nous donne et en remplaçant à la fois R0 par la résistance de l’ampoule à 20°C et delta T par l’élévation de température (2700-20).
On peut calculer la valeur de la résistance du filament à chaud :
R=60 x (1+ 0.0044×2680)
R=60 x (1+ 11.792)
R=60 x 12.792
R=767 ohms
Cette valeur est très proche de celle calculée plus haut à partir des caractéristiques annoncées par le fabricant.
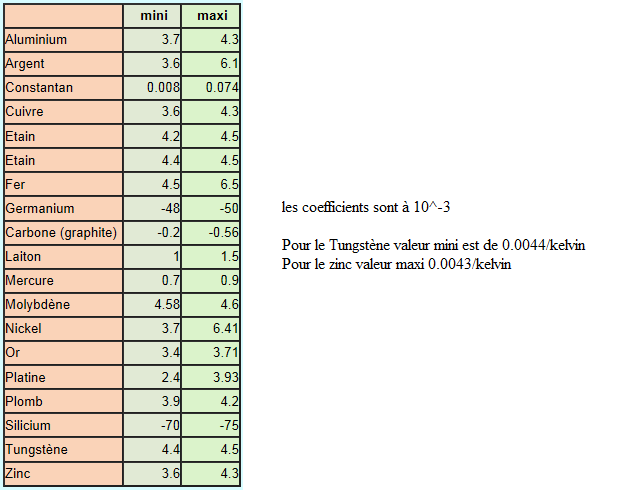
Coefficient de température par kelvin
Une application pour la mesure des températures
Les principes utilisés pour la réalisation de sondes thermométriques sont variés (thermocouples, thermistances…). Une sonde parmi les plus populaires est celle qui est basée sur le coefficient de température d’un fil de platine. Il en existe plusieurs variantes dont l’une, baptisée Pt100 qui permet des mesures de températures pouvant aller de -200°C à plus de 800°C.
La Pt100, comme son nom l’indique un peu présente une résistance de 100 ohms à 0°C. Pour une variation de tepérature de 1°C, la variation correspondante de résistance de la sonde est de 1,393 ohms (ou 1,384 selon le modèle). Ainsi, à 100°C, la résistance de la sonde sera de 139,3 ohms.
Sa linéarité est très bonne, ce qui permet de l’utiliser directement dans un pont et de calculer facilement la température correspondant à la tension délivrée