Théories transistor JFET (calculs/amplification…)

Présentation

Dans cet article nous allons faire le point sur des théorèmes qui seront important à comprendre afin de pouvoir réaliser différents montages comme amplificateur en tension ou bien celui d’in interrupteur électronique.
Tout d’abord le transistor JFET, est un transistor qui fait parti de la famille des transistors à effet de champ (FET : Field Effect Transistor). Le transistor MOSFET appartient également à cette famille.
Le but de cette article et de comprend l’aspect physique de ce composants et de savoir l’utiliser dans un montage électronique.

Un transistor JFET possède trois bornes :
la grille (g)
le drain (d)
la source (s)

Il existe deux types de transistors JFET :
Canal N et canal P (NJFET et PJFET)

Pour un JFET à canal N en fonctionnement normal :

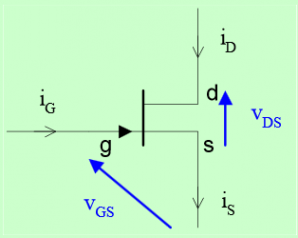
Pour un JFET à canal N en fonctionnement normal le fléchage du courant est tension est indiqué de cette forme et devra être appliqué pour n’importe quel cas de figure.
– la tension Vds est positive
– la tension Vgs est négative ou faiblement positive (< 0,6 V)
– le courant de grille est quasiment nul ig=0
– le courant entre dans le transistor par le drain (id)
– le courant sort du transistor par la source (is)
– Loi des nœuds : id=is

Interprétation du fonctionnement JFET

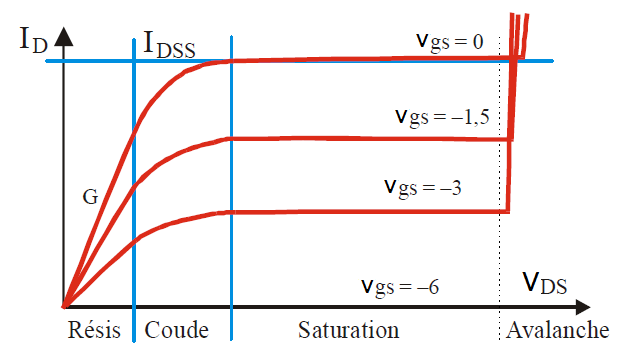
Zone Ohmique
La zone ohmique pour le transistor JFET permet d’exploiter ce qu’on appel le RDS(on) du transistor JFET c’est-à-dire que pour des tensions VDS faibles, le canal se comporte comme une résistance ohmique., le JFET est alors équivalent à une résistance commandée par la tension Vgs.Pour une valeur VP (tension de pincement) qui est suffisamment négative de Vgs (Vp=Vgs(off) souvent indique dans le document constructeur ou dataSheet)). Il en résulte que la conduction s’annule, et on dit alors que le canal est « pincé », et dans ce cas il correspond à un interrupteur ouvert (Id=0A).</span

Zone du coude
Pour faire simple le JFET arrive à un moment donné qu’il va saturer.
Zone de saturation
Dans cette zone le courant du drain reste constant et le transistor est dit saturé.
La valeur maximum de ID pour VGS = 0, est notée IDSS de même cette valeur est donné dans la doc constructeur.
Zone d’avalanche
Elle résulte d’un claquage inverse de la jonction drain-grille. Ce claquage est destructeur du Dispositif si rien ne limite le courant drain.

Interrupteur électronique

Exemple avec le JFET 2N3819


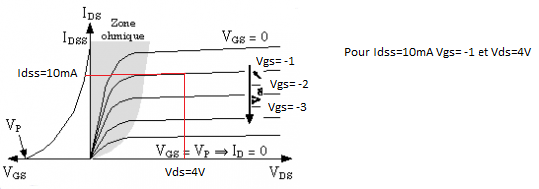
(Clique pour agrandir )

Doc constructeur ou DataSheets

(Clique pour agrandir )

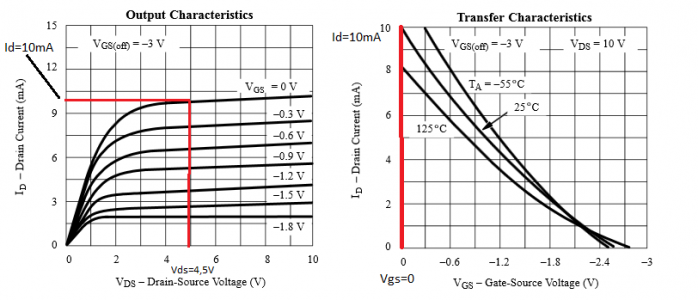
Comme nous l’avons vu précédemment, Vgs permet dans la zone linéaire (ou zone ohmique) de commander le transistor JFET grâce à la tension Vgs et cela va aussi en parallèle de “jouer” sur sa résistance RDS(on). La tension Vgs permettra dans cette configuration en mode linéaire de modifier le courant id qui circule dans le transistor et de modifier sa résistance “interne”.
Le constructeur nous indique que pour le 2N3819, le courant id est maximal lorsque id=idss pour Vgs=0V, c’est-à-dire que Idss typique =10mA et que Idss Max = 20mA. Pour ma part et c’est mon avis personnel afin de ne pas détruire mon transistor j’ai décidé de prendre un Idss=10mA.
Le constructeur indique aussi que pour une tension Vgs< Vgs (off) avec Vgs(off)=-3V , on peut considérer que le courant id est nul(< 10 nA) : le transistor est bloqué (off) on peut symboliser le transistor JFET par un interrupteur ouvert.

Le transistor fonctionne en commutation (2 états)

– Lorsque la tension Vgs <= Vgs (off), le transistor est bloqué id=0 (Interrupteur ouvert).
– Lorsque la tension Vgs =0 , le transistor fonctionne dans la zone ohmique, et se comporte comme une résistance Rds(on) (Interrupteur fermé).
Bon!! Et bien maintenant que nous connaissons Idss ainsi que Vp nous pouvons maintenant voir comment utiliser le JFET en mode amplificateur cela vous donne envie?.

Amplificateur de tension

Un montage amplificateur permet comme son nom l’indique d’amplifier un signal. Ainsi avec un petit signal en entrée nous allons nous retrouver en sortie avec un plus grand signal soit plutôt une amplitude plus importante.
En règle générale, l’amplification de ces signaux proviennnent d’un signal alternatif comme par exemple un micro, un amplificateur, un piezzo, et bien d’autres choses encores….
 
Ce qui est intéressant avec un JFET c’est que sont impédance d’entrée est très grande et aucun courant ne peut donc traverser sa grille (Ig donné par le constructeur est en pico ampère !!! donc négligeable).
En électronique nous sommes très souvent confronté à mélanger des signaux alternatif et continu et il est donc important de savoir comment les séparer. C’est d’ailleurs ce que nous allons voir sans plus attendre.

Exemple 1)

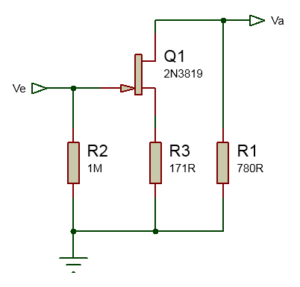
L’entrée est représentée par Ve et que cette tensions correspond à une tension alternative. La sortie quant à elle est représentée par Vs qui sera ici la tension Vs=Ve*G (avec G qui correspond ici dans cet exemple au Gain du montage). Les composants déjà positionnés sur le schéma électronique ne sont pas mis au hasard et nous allons les calculer ensembles.

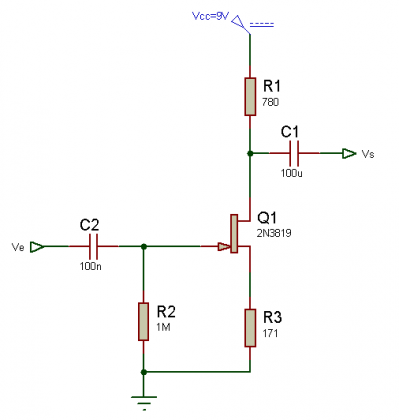
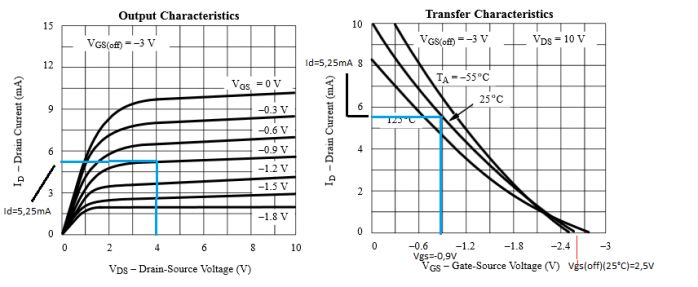
En continu…

Calculs des courants de repos
Les courants de repos sont les courants de polarisation de notre montage et ces courants sont toujours calculer en continu, il s’agit en définitive du courant permanent qui circules.
Afin de déterminer ces courants de repos il faut donc simplifier le montage à savoir que lorsque nous raisonnons en continu, il faut :

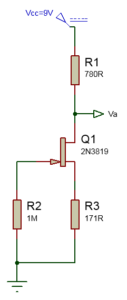
Voilà maintenant ce qu’il nous reste de notre circuit !! Et bien reste plus qu’à calculer ces fameux courant de repos c’est parti !!!
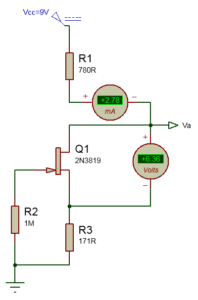
Fixons nous arbitrairement dans un 1er temps le courant que nous désirons faire circuler entre R1 et R3 soit Id=Is = 5,25mA si Id=5,25mA Vgs= ?, ohh !!!Et bien je vais prendre un Vgs je sais pas moi allez disons -0,9V peut-importe c’est aussi arbitraire.
Maintenant que nous avons fixé ce courant de repos à 5,25mA, je vais me diriger du côté de Vgs et pouvoir déterminer la résistance R3.

Calculs de R2
Pas de tension aux bornes de R2 je mets arbitrairement une résistance de 1M nous verrons sont impact en alternatif

Calculs de R3
VR2-Vgs-VR3=0 soit VR3=VR2-Vgs=0-(-0,9) = 0,9V tension aux bornes de R3
R3=09/0,00525=171,41Ohms
Potentiel Va :
En général le potentiel Va est fixé à Vcc/2 soit 9/2=4,5V. ceci est primordial afin d’éviter la saturation du signal et que celui-ci soit écrêté.
Sachant que VR3=0,9V, et que si Vds=4V Va=4,9V (Va=VR3+Vds), nous somme proche des 4,5V

Calculs de R1
R1=(Vcc-Va)/id=(9-4.9)/0,00525=780 ohms

En Alternatif…

Bon, ok!! je suis d’accord la simulation n’est pas proche des calculs mais nous avons quand même une approche même si ce n’est pas parfait !!!
Maintenant que nous avons déduit les courants de repos pour la source continu, passons du côté de l’alternatif.
Le raisonnement en alternatif devient cette fois-ci:

Et voila ce que donne le schéma en alternatif. Mais Nous allons dévoiler un 3ème schéma qui celui-ci permet de prendre en compte la variation des signaux de petit voir moyennes fréquences. Et nous allons représenter dans ce nouveau schéma des générateurs de courant.

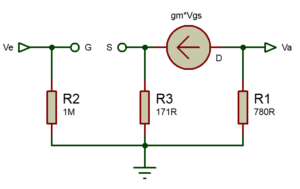
Schéma aux petites ou moyennes variations de fréquences

Nous retrouvons sur ce schéma G=Grille, S=Source, D=Drain, ainsi qu’une source de courant fournissanr un courant qui circule en boucle en effectuant le chemin suivant
Gm*Vgs -> R3 -> masse -> R1 -> gm*Vgs -> R3 -> tec…. .
Le but de ce montage est de déterminer en alternatif le gain de ce montage et c’est ce que nous allons tout de suite.
Le potentiel Va =gm*Vgs*R1 mais attention puisque le courant est dans le même sens que la « flèche de la d.d.p » (différence de potentiel entre le point Va et la masse), il en résulte que nous sommes dans une convention en générateur soit Va= -gms*Vgs*R1 (le signe moins correspond à un générateur).
On peut donc dire que la tension de sortie représente le potentiel Va.
En ce qui concerne la tension d’entrée Ve quant à elle celle-ci est égale à Ve – Vgs – VR3=0
(une source de courant n’est pas une source de tension on ne peut donc pas établir une loi des maille en faisant:
Ve – Vgs – V(gm*Vgs)- Va !!! )
Après cette petite parenthèse, revenons sur Ve – Vgs – VR3 = 0 ce qui donne que Ve = Vgs – VR3
VR3 = R3*I3 = R3*gm*Vgs
Ce qui nous donne que
Ve = Vgs ( 1 +gm*R3)
Vs=Va=-gms*Vgs*R1

Calcul du Gain
Pour finir le gain est donc égale à
Av=Vs/Ve=- (gm*R1)/(1+(gm*R3))
C’est quoi gm?!!
Bon ok!! Le calcul de gm correspond à la transconductanceet sont calcul est le suivant :Gm=(-2/Vp)*racine carré de (Idss * Id repos)
Il en résulte que nous connaison Vp=Vgs(off)=-3V, Idss=10mA et Id repos=5,25mA alors
Gm=((-2/-3)*racine carré de (0,010* 0,00525) = 0,00483
Av=Vs/Ve= (0,00483*780)/(1+(0,00483*171))=2,06
Il est aussi intéressant de savoir qu’il est possible aussi d’augmenter le gain en ajoutant un condensateur en parallèle sur la résistance R3 (condensateur non représenté sur le schéma électronique)

Calcul condensateur de découplage

 

 
Nous avons bientôt fini, il ne reste plus qu’a calculer les condensateurs C1 et C2 afin que tous ce qu’il se passe entre ces 2 condensateurs reste entre ces 2 condensateurs !! Oui vous l’avez compris les courant et tension de repos ne doivent en aucun cas sortir soit par Ve soit par Vs et c’est pour cette raison que nous faisons appel à des condensateurs de découplages.
 
Calcul de C2
Si nous regardons l’assemblage de C2 avec R2, nous avons un filtre passe haut d’où F=1/(2*3,14*Fc*R1*C1) , C1 est donc égale à C1= 1/(2*3.14*Fc*R1) . J’ai décidé de prendre une fréquence de coupure (Fc) de 50Hz, c’est-à-dire que tous les signaux qui auront une fréquence supérieur à 50Hz celle-ci devra passer dans le montage électronique sinon le reste sera bloqué.
C1=1/(2*3.14*50*1000000)=3nF (je décide prendre 100nF ce sui donnerais une fréquence de coupure de 1,59Hz

Calcul de C1
Même principe mais cette fois-ci dans l’autre sens. Imaginons qu’on applique une tension d’entrée sur la sortie (oui bien entendu c’est théorique je ne le ferais pas !!).
à C1= 1/(2*3.14*Fc*R1)
C1=1/(2*3.14*1,59*1000000) = 100nF (pareil j’ai décidé de mettre une Fc=1,59Hz ce qui donne 100nF
Si pour une tension crête de 1V nous avons en entrée, en sortie nous obtiendrons Vs=Ve*2,06 soit 2,82V crête.

Test sur prototype

Le montage qui suis a été testé sur plaque d’expérimentation sans soudure. Le transistor JFET de type 2N3819 est raccordé comme le montre le schéma électronique ci-dessous


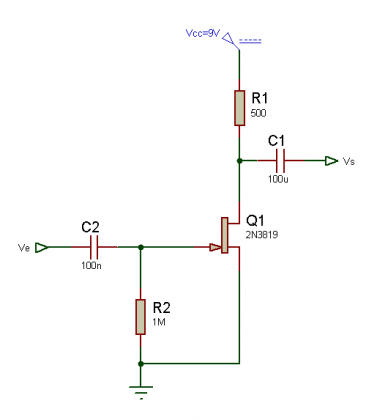
Nous avons vue précédemment pour un courant d’environ 5mA le gain était de 2,06, et bien nous allons maintenant mettre un courant plus important c’est-à-à-dire le double soit 10mA et voir comment va se comporter notre nouveau gain.
Prenons toujours le potentiel du drain à Vd=VCC/2=9/2=4,5V, ainsi pour une tension Vgs=0V le courant maxi est de 10mA (environ d’après le graphique courbe rouge). Dans cette situation pour un courant de 10mA la chute de tension sera de 4V (là encore nous somme proche des 4,5V).
R1=(9-4,5)/0,010=450 Ohms (500 Ohms)
Calculs de la transconductance (gm) soit :
gm=(-2/Vp)*racine (Idss*Id(repos))=(-2/-2,5)* racine (0,010*0,010)=0,008mmohm
le gaine est donc égale à :
Av=Vs/Ve= – (gm*R1)/(1+(gm*R3))=(0.008*500)/(1+(0.008*0))= – 4
Vs= – 4*Ve

Proto en photo
Le calcul suivant donne Vs= – 4*Ve

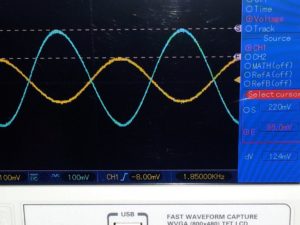
la 3ème photo montre en sortie (S) un signal de 220mV crête pour une tension d’entrée (E) de 92mV crête (environ 150mV), la aussi l’écart est dû à la dispersion des caractéristiques du transistor.