Détermination de la charge
Prenons l’exemple de la norme UTE 15-105
Une charge qui consomme un courant d’emploi Ib=140A sous 230V 50Hz, pour un cos Fi le déphasage entre la tension et le courant est d’environ 36 ,87° (le courant est en retard de 36,87° sur la tension la charge est donc inductive)
Cos fi=0,8
Sin fi=0,6
P=U.I.cos Fi=230*140*0,8=25760W
Q=U.I.sin Fi=230*140*0,6=19320VAR
S=U.I=230*140=32200VA
D’après la puissance nous savons que seul une résistance consomme de la puissance active, et que seulement une bobine ou condensateur consommes de la puissance réactive.
P=R.I² => R=(P/I²)=25760/140²=1,314 ohms
Q=XL.I² => XL=Q/I²=19320/140²=0,9857 ohms L=XL/2.pi.50=(0,9857)/(2.pi.50)=3,1mH
L’impédance Z du circuit est donc Z=racine (1,314²+0,9857²)=1,64 ohms
Cos Fi=R/Z=1,314/1,64=0,8 ohms (environ)
La représentation est donc une charge R.L. avec une résistance de 1,314Ohms en série avec une bobine de 3,1mH
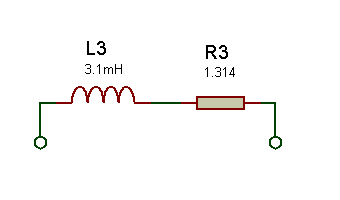
Calcul d’une chute de tension
Parlons maintenant de la chute de tension, qui ce détermine par la fonction :
u=k[(Ro*(L/S)*cos Fi)+(lambda*L*sin Fi)]*Ib
u = en volts
k = 1 pour du triphasé
k = 1 pour du monophasé
Ro = 0,023 ohms/mm² (résistivité des conducteurs)
Lambda = 0,08 mohms/m => 0,00008ohms/m (même unité de mesure)
Ib étant le courant d’emploi dans le circuit. (140A pour notre exemple)
Cos Fi et Sin Fi correspond au déphasage de la tension V par rapport au courant I
Puis nous rajoutons la chute de tension relative exprimé en % delta U=100*(u/U0) avec U0 la tension entre phase et neutre.
la résistance représente (Ro*(L/S)) =(0,023*(110/35))=0,072 ohms
la réactance représente (lambda*L) =(0,00008*110)=0,088 ohms
pour la phase nous avons une résistance de 0,072 ohms et une réactance de 0,088 ohms et pour le neutre c’est la même chose.
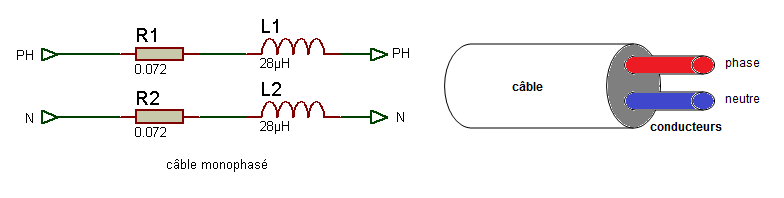
en ce qui concerna la chute de tension dans ce câble: u=2[(0,023*(110/35)*0,8)+(0,00008*110*0,6)]*140=17,67V, puis delta U=100*(17,67/230)=7,68%
Alimentation de la charge
Si nous alimentons la charge par l’intermédiaire de ce câble monophasé d’une longueur de 110m et en prenant un voltmètre position AC, et que nous mesurons la tension à ses bornes nous avons une tension de :
Uréseau-Delta U=230-17,67=212,33V (environ, 213V)
Nous avons bien une chute de d’environ 7% aux bornes de notre charge (R3 en série avec L3)
(D’ailleurs pour 7% cela nous donne une tension d’environ 213V aux bornes de la charge),Mais ???? le courant alors n’est plus de 140A ? la tension aux bornes de la charge est de 213V donc le courant
I=U/Z=213/1,64=129A (nous sommes pas à 2A près…)
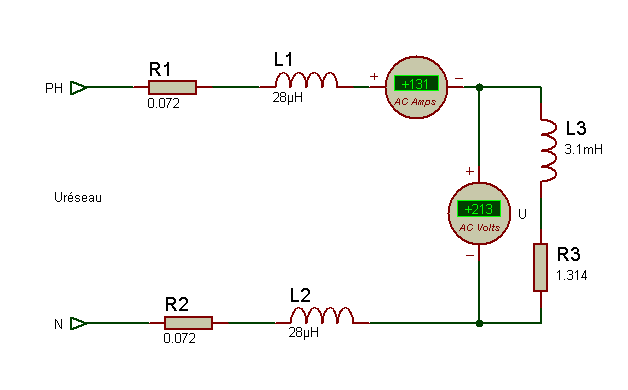
Autre manière de calculer une chute de tension
Pour la Phase
Pour les matheux en étant puriste sur l’ensemble de l’installation le calcul serais différent évoqué comme ci-dessus mais le résultat et quand même proche du précédent
Reprenons :
résistance de la charge 1,314ohms
réactance de la charge 0,9857 ohms
résistance de la phase et du neutre (2*0,072)=0,144 ohms
réactance de la phase et du neutre (2*0,0088)=0,0176 ohms
la résistance total vue par le réseau est égale à Rt=R1+R3+R2
Rt=0,072+1,314+0,072=1,484 ohms
la réactance total vue par le réseau est égale à Xt=X1+X3+X2=L1w+L3w+L2w
Xt= 0,0088+0,9857+0,0088=1 ohm (L=3,2mH)
L’impédance vue par le réseau est égale à Zt=racine (Rt²+Xt²)=racine (1,484²+1²)=1,789ohms
Le courant est donc I=U/Z=230/1,789=128,52A (proche de 129A).
La représentation est alors comme la synoptique ci-dessous:
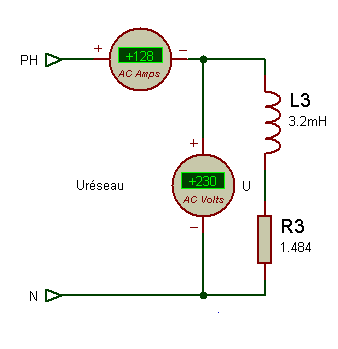
Fresnel
Bon maintenant utilisons les vecteurs de fresnel, la tension du réseau est en phase avec l’origine cos Fi=0 (pas de déphasage), le courant qui traverse le câble et la charge lui est en phase avec la résistance du câble et la résistance de la charge (pas de déphasage courant tension purement résistif).
La chute de tension aux bornes de UR=R*I=0,072*128,52=9,25V
La chute de tension aux bornes de UL=Xl*I=0,0088*128,52=1,13V
La chute de tension entre A et N est égale à
UA(résistif)=UPH-UR=230-(0,072*128,52)=220,7V (pour le résistif) (223V)
UA(inductif)=UL=0,0088*128,52=1,13V (pour l’inductif) (1,05V)
UA/N (A par rapport au neutre)=racine (UA(résistif)²+UL(inductif)²)=racine (220,7²+1,13²)=220V
la différence entre PH et A est égale à 230-220=10V environ (soit 9,25V pour être précis mais bon….)
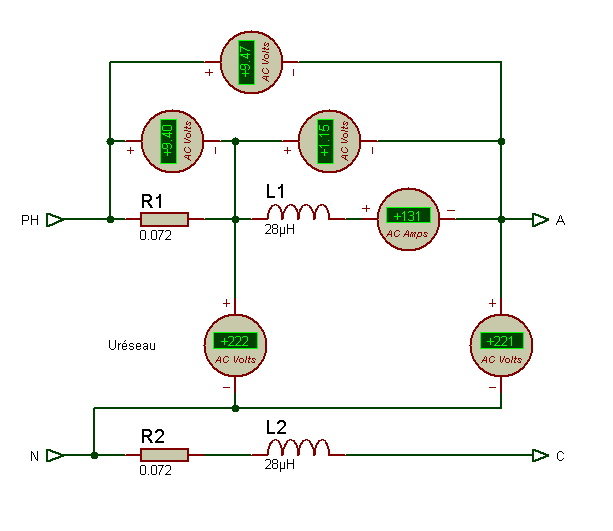
Effectivement si on prend les valeurs mesurées les calculs sont identiques aux mesures j’ai préféré rester sur mes valeurs….
U(PH/A)=racine (UR²+UL²)=(9,40²+1,15²)=9,47V UA/N(point A par rapport au neutre)=230-9,47=220,53 (221V)
Pour le neutre (N)
Puisque le conducteur de Phase est identique au conducteur de neutre suffit de multiplier par 2 la chute de tension dans le conducteur du neutre pour trouve la trension aux bornes de la charge, avec une chute de tension de 10 soit 10*2=20V et 230-20=210V (avec 9,25V cela donne 18,5V soit 230-18,5=211,5V ouff!!!)
La tension aux bornes de notre charge est de d’environ 212V mais…. c’est pas ce que nous avons trouvé au début à quelque chose près?
Suppression de la chute de tension
Bon, d’accord nous avons fait tous ces calculs pour démontrer la chute de tension aux bornes de la charge mais nous avons pas supprimeé cette chute de tension, le principe va être simple il suffit d’augmenter la section de notre câble, si on décide d’avoir une chute de tension nul mais pas complétement aux bornes de la charge cela veut dire que:
u=k[(Ro*(L/S)*cos Fi)+(lambda*L*sin Fi)]*Ib=0
et donc :
Ro*(L/S)*cos Fi= – lambda*L*sin Fi
La résistance est égale à :
Ro*(L/S)=(- lambda*L*sin Fi )/cos Fi
=(-0,00008*110*0,6)/0,8= – 0,0066 hum!!! (0,0066 c’est mieux j’ai jamais vue une résistance négative mais la simuler oui enfin c’est autre chose.)
Donc 0,0066=Ro*(L/S) alors S=Ro*L/(0,0066)=(0,023*110)/0,0066=383mm² !!!
Notre nouvelle chute de tension est donc:
u=2[(0,023*(110/383)*0,8)+(0,00008*110*0,6)]*140 = (environ 2,95V)
230-2,95=227V et nous avons un courant de (227/1,64)=138A mieux que 129A (10A de mieux).
la chute de tension relative en % donne U(%)=100*(2,95/230)=1,28% dans certaines normes elle est réglementaire pour l’éclairage inférieur à 3%, dans ce cas pour respecter cette valeur inférieur à 3% il est conseiller d’augmenter la section du câble entrainant une diminution de la chute de tension.