Le condensateur
Le condensateur est un composant électronique élémentaire, constitué de deux armatures conductrices (appelées « électrodes ») en influence totale et séparées par un isolant polarisable (ou « diélectrique »). Sa propriété principale est de pouvoir stocker des charges électriques opposées sur ses armatures. La valeur absolue de ces charges est proportionnelle à la valeur absolue de la tension qui lui est appliquée.
Le condensateur est utilisé principalement pour :
Stabiliser une alimentation électrique (il se décharge lors des chutes de tension et se charge lors des pics de tension) ;
traiter des signaux périodiques (filtrage…) ;
séparer le courant alternatif du courant continu, ce dernier étant bloqué par le condensateur ;
stocker de l’énergie, auquel cas on parle de supercondensateur.
Formule avec i = C(du/dt).
Le condensateur est caractérisé par le coefficient de proportionnalité entre charge et tension appelé capacité électrique et exprimée en farads (F). La relation caractéristique d’un condensateur idéal est :
i = C(du/dt).
où :
i : désigne l’intensité du courant électrique qui passe par le composant, exprimée en ampères (symbole : A) ;
u : la tension aux bornes du composant, exprimée en volts (V) ;
C : la capacité électrique du condensateur, exprimée en farads (F) ;
du/dt : la dérivée de la tension par rapport au temps (V/s).
Les signes sont tels que l’électrode par laquelle entre le courant (dans le sens conventionnel du courant : + vers -) voit son potentiel augmenter.
Formule avec Q = CU.
Il est possible aussi de calculer la quantité de charge accumulée par le condensateur, on définit la capacité par la relation:
Q = CU
où :
Q : est la charge stockée sur sa borne positive (qui s’exprime en coulombs),
C : la capacité électrique du condensateur (farads),
U : la tension aux bornes du composant (volts).
Théorème de Millman
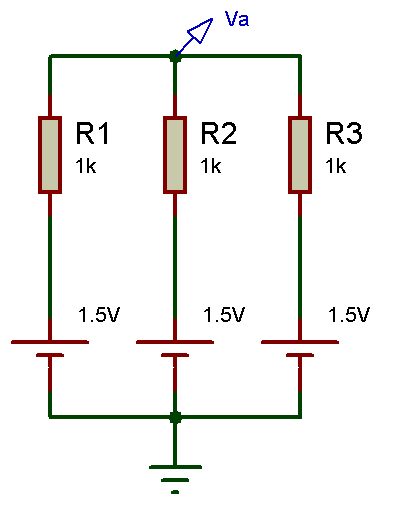
Le théorème de Millman est une forme particulière de la loi des nœuds exprimée en termes de potentiel, il est tout à fait possible d’exprimer le potentiel Va par le théorème de Millam qui est a l’honneur de l’électronicien américain Jacob Millman.
Dans un réseau électrique de branches en parallèle, comprenant chacune un générateur de tension parfait en série avec un élément linéaire, la tension aux bornes des branches est égale à la somme des forces électromotrices respectivement multipliées par l’admittance de la branche, le tout divisé par la somme des admittances. oui est c’est à dire ??!
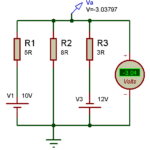
Sur le schéma ci-dessus, la tension représentative a été calculée en suivant la formule du théorème de Millman:
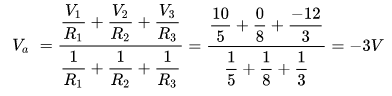
Le signe négatif signifie que la tension au point Va est négative par rapport à la masse commune.
Remarque: Il n’est pas nécessaire que les sources de tension soient parfaites, celles-ci peuvent inclure des résistances même de forte valeur.
Calculs des surtensions aux bornes d’un condensateur
Ce que je vous propose, c’est de voir ensemble l’illustration ci-dessous , et de faire des calculs en utilisant le théorème de Millman pour arriver à déterminer des potentiels “volants” sur des points particulier d’un circuit électronique. Je me passerais des formules abracadabrantes surtout au niveau des régimes transitoires ou nous allons pas commencer à faire des calculs sur les équations différentiels du 1er ordre ou bien en passant par les transformées de Laplace. Oui! on peut le faire mais je vous épargne tous ces calculs. Le but est de comprendre comment se comporte un condensateur lorsque celui-ci est soumis à différents potentiels, ou lorsque ces potentiels vont changer subitement. Nous verrons pas à pas et en détails ces calculs afin de voir que le condensateur n’admet aucun changement d’état brusque de tension au niveau de ses bornes et c’est pour cette raison que le condensateur s’oppose à toutes variations brusques de tension. (Les variations de tensions sont limitées via le du/dt).
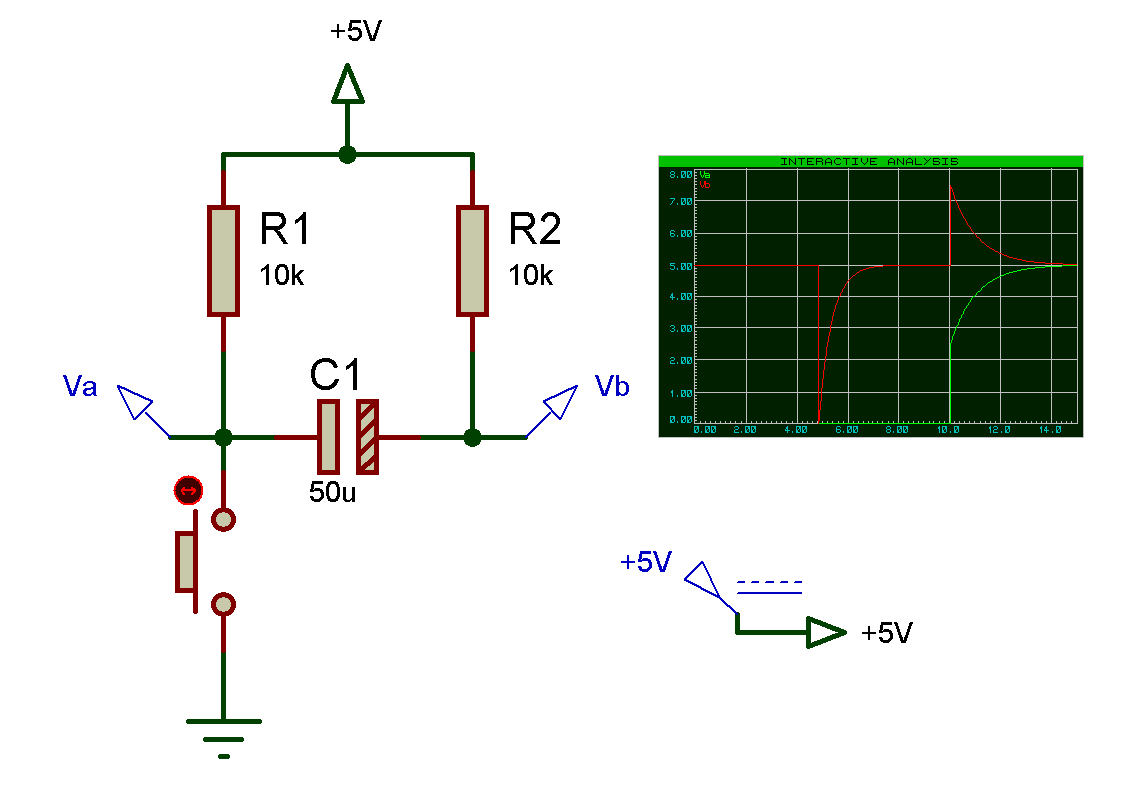
(Clique pour agrandir)
Etude complète
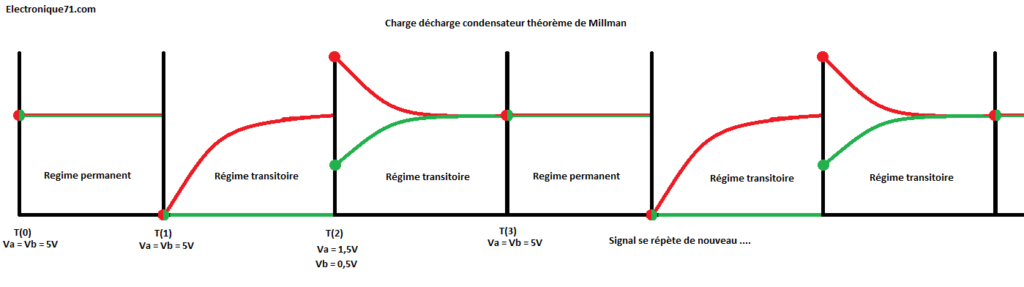
Avant la mise sous tension (interrupteur ouvert) – T(0) Va=Vb=5V
Avant la mise sous tension, l’interrupteur est ouvert, et le condensateur quant a lui est complétement déchargé la tension entre ses bornes Uc = Va – Vb = 0V. Cette tension étant nulle, on peut donc dire que Va = Vb, et pour aller plus loin, je peut représenter le condensateur comme un fil électrique (voir ci-dessous).
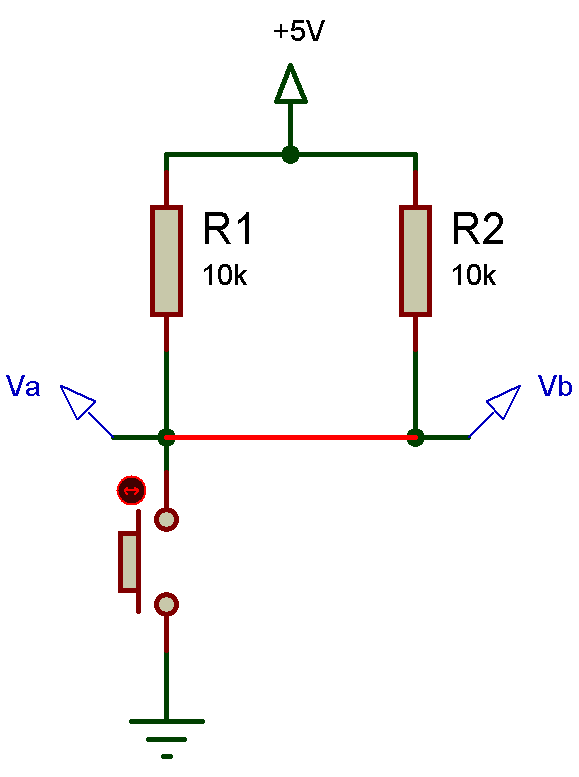
J’espère que vous me suivez toujours ? La tension étant nulle à ses bornes c’est comme si je vous demandais de mesurez la tension aux bornes d’un interrupteur lorsque celui-ci est fermé , le voltmètre affichera 0V (un interrupteur fermé correspond à un fil et donc pas de différence de potentiel lorsque nous mesurons 1 fil électrique).
Ceci étant dit au passage, il n’y a pas de courant qui circule non plus!! Oui, le courant va partir du +5V de l’alimentation pour retourner d’où il vient c’est à dire au pôle négatif de l’alimentation qui est représenté par une masse… Or l’interrupteur est ouvert !!
Si le courant est nul, la différence de potentiel entre la source qui est le +5V et le potentiel Va = Vb est égale à la tension elle même car:
UR1 = R1 * i = 1K * 0 = 0V
Va = 5 – UR1 = 5 – 0 = 5V
Comme Va = Vb alors Vb = 5V
Ainsi nous avons déterminé à T(0) que Va = Vb = 5V les tensions sont “superposées” l’une sur l’autre comme le montre le graphique que j’ai réalisé. tant que je ne ferme pas l’interrupteur la tension restera à 5V jusqu’au moment ou je vais appuyer dessus à l’instant T(1)
Après la mise sous tension (interrupteur fermé) – T(1) Va=Vb=0V
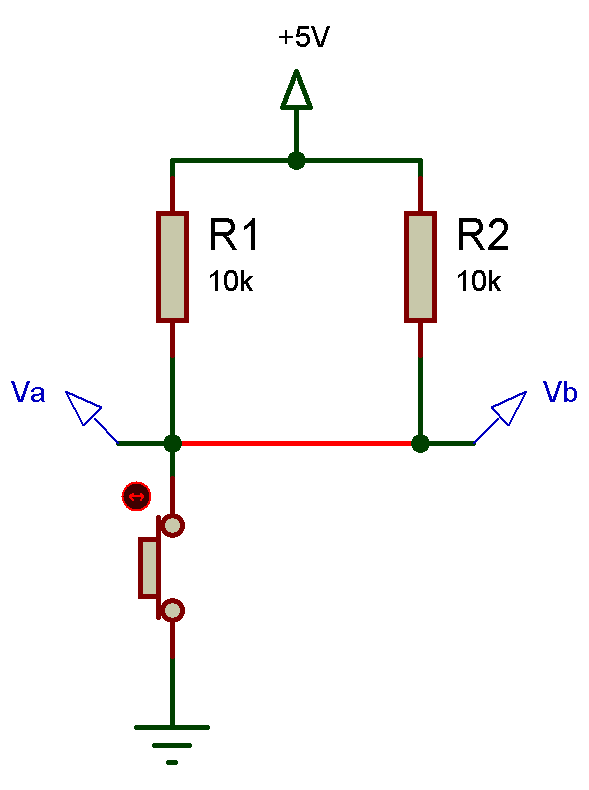
Cette fois-ci je vais appuyer sur l’interrupteur, mais à t(1) le potentiel Va est imposé par la masse soit Va=0V le condensateur n’a pas eu le temps pendant dans cette transition de fermeture d’interrupteur de se charger il en résulte que le condensateur correspond toujours à un fil et la tension Vb = 0V car Va = Vb. Laissons maintenant un peu de temps au condensateur de se charger dans la phase que l’on nomme un régime transitoire.
Après la mise sous tension (Condensateur complétement chargé) – T(2) Va=2,5V et Vb = 7,5V
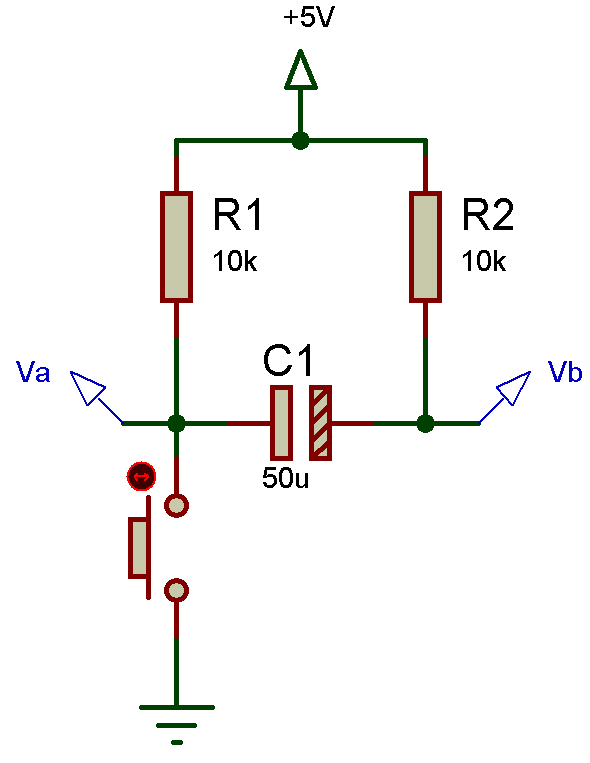
Je vous vois venir pourquoi Va = 2,5V et Vb = 7,5V ??!
Lorsque le condensateur va être complétement chargé (comme dis précédemment nous étudierons pas le régime transitoire suite aux calculs un peu plus lourd), nous somme façe à une situation ou Va et Vb se retrouve à des potentiels “volant” et dans ce cas nous ne ne connaissons plus la tension Va = ? V, et la tension Vb = ? V.
C’est à ce moment précis que nous allons faire appel au théorème de Millman qui est un outil extrêmement puissant (d’ailleurs mon préféré que Norton ou Thévenin) pour résoudre ce genre de situation afin de déterminer des potentiels précisemment.
Les seules tensions connues dans le circuit sont la tension d’alimentation 5V, ainsi que la tension aux bornes du condensateur Uc = 5V (oui le condensateur à été chargé à 100%) or quand est-il pour Va et Vb ? c’est ce que nous allons voir de suite:

Nous devons respecter le Théorème de Millman ou nous avons toujours une tension sur une résistance (V/R) ce qui nous donne (j’ai réalisé une capture de mrd calculs c’est beaucoup mieux je trouve comme ça…

Nous avons trouver Va super!! il ne reste plus qu’a en déduire Vb en faisant simple:
Uc = Vb – Va ce qui nous donne Vb = Uc + Va = 5 + 2,5 = 7,5V et voilà notre surtension!!
Modification du schéma
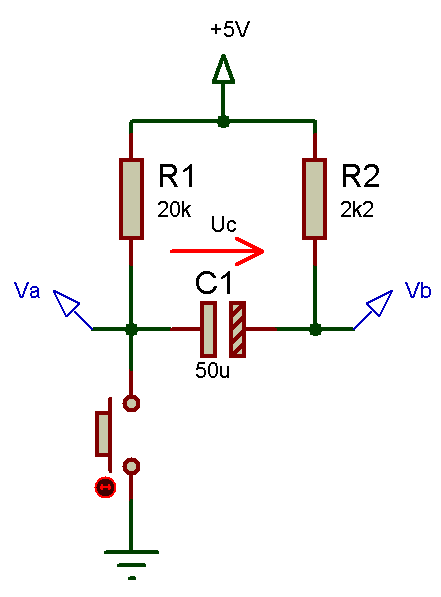
J’ai changé la valeur des résistances avec R1 = 20Kohms et R2=2,2Kohms. Niveau calculs j’obtiens:
Va = E * R2/(R1+R2) = 5 * (2200/22200) = 0.4954V
Vb = Uc + Va = 5 + 0,4954 = 5,4954V
Pour Info : J’ai repris la formule générale détaillée dans ma note de calcul ci-dessus formule en rouge.
Pour le reste je vous laisse réflechir un peu 😉 vous devez trouver Va = E * (R2/(R1+R2)).
Graph

(Clique pour agrandir)